Problème 517 – Le cycle des coffres de Squad Busters

Niveaux : 2 versions : Cinquième (ou fin de Sixième) / Terminale (Spécialité Maths)
Chapitres : Arithmétique (5^ème) / Probabilités, Loi binomiale, Logarithme népérien (Terminale)
Inédit, publié le 09/03/2025

Né en 2024 dans l’univers de Supercell, l’éditeur de Clash of Clans, Clash Royale ou encore Brawl Stars, Squad Busters regroupe les personnages de ces jeux iconiques pour proposer un jeu frénétique de combats multi-joueurs. Le principe : former son équipe de personnages pour aller piller des ressources et combattre d’autres équipes dans des matchs. Tout comme dans Clash Royale, un des objectifs du jeu est d’obtenir des personnages de plus en plus évolués : pour cela, les joueurs obtiennent des récompenses, les fameux coffres, dont le type (commun, rare ou épique) ne va pas dépendre du hasard, mais d’un cycle précis que nous allons étudier ici.

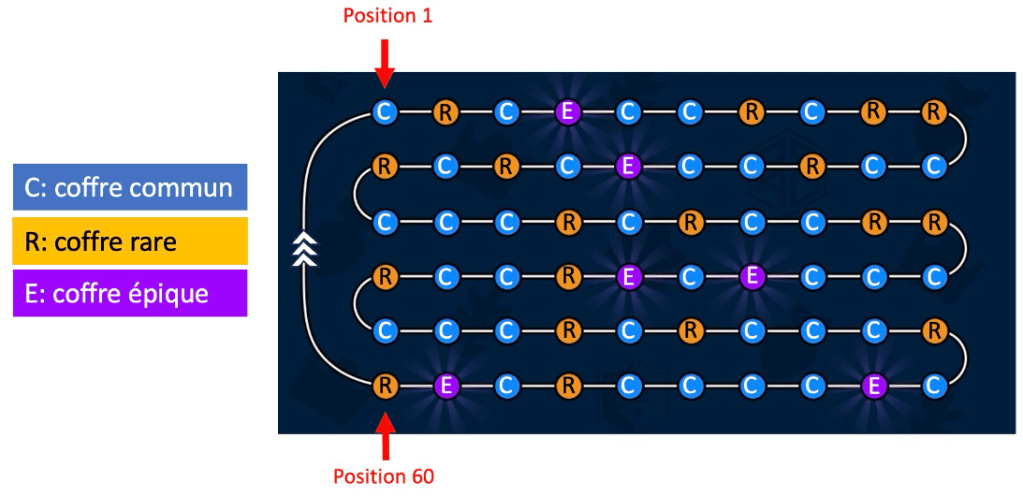
Ce cycle, publié par Supercell⁽¹⁾ et reproduit en Annexe, s’étale sur 60 coffres – 36 communs, 18 rares et 6 épiques – sachant qu’un coffre épique est évidemment celui le plus recherché, car il est le moins fréquent et offre les meilleurs personnages. Connaître sa position dans le cycle permet de savoir quel type de coffre on va obtenir après un match.

Les deux problèmes sont strictement indépendants.

Niveau Cinquième

Pour l’intérêt de ce problème, on a numéroté en Annexe les positions dans le cycle (en indiquant la position 1 et 60 ainsi que le sens du cycle), mais cela ne veut pas dire forcément que le premier coffre ouvert par un(e) joueur(se) quelconque est celui situé en position 1.

1) Selon le document en Annexe, à quelles positions dans le cycle se trouvent les 6 coffres de type épique?

2) On suppose que Mia commence à jouer à Squad Busters, et que son premier coffre ouvert est celui situé en position 43.

a) Quel sera le type du coffre qu’elle obtiendra quand elle ouvrira son 1000^ème coffre ? Justifier la réponse.
b) A ce moment-là, combien aura-t-elle alors ouvert de coffres de type épique en tout ?

3) a) Au bout de combien de coffres ouverts Mia se retrouvera-t-elle à la position 1 du cycle pour la 50^ème fois ?
b) Au bout de combien de coffres ouverts Mia aura-t-elle atteint les 500 coffres de type rare?

4) A un moment, Mia s’est perdue dans le cycle. Elle remarque cependant qu’elle vient d’ouvrir un coffre de type épique, et qu’elle en avait ouvert un du même type exactement 100 coffres juste avant. A quelle position du cycle Mia se trouve-t-elle alors ?

Niveau Terminale

1) Tim, un lycéen qui joue souvent à Squad Busters, ignore sa position dans le cycle. Suite à un match qu’il remporte, il ouvre successivement deux coffres d’affilée (qui se suivent donc dans le cycle).

On nomme les évènements suivants :
C₁(resp. C₂): Tim ouvre un coffre commun pour le premier coffre (resp. pour le deuxième).
R₁(resp. R₂): Tim ouvre un coffre rare pour le premier coffre (resp. pour le deuxième).
E₁(resp. E₂): Tim ouvre un coffre épique pour le premier coffre (resp. pour le deuxième).

Remplir l’arbre ci-dessous qui modélise la situation (écrire les probabilités sous forme de fractions irréductibles).

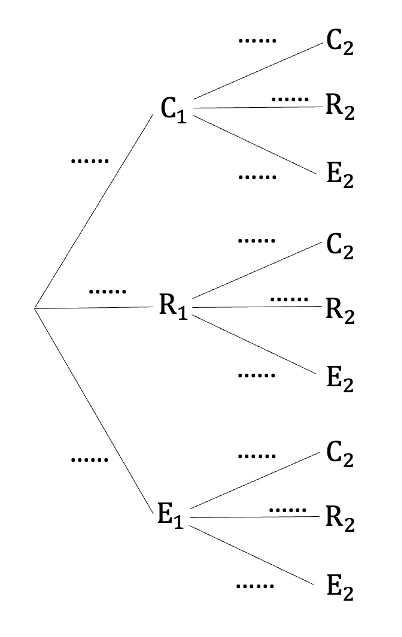
2) a) Quelle est la probabilité que parmi ces deux coffres, l’un soit de type épique ?
b) Montrer que la probabilité que Tim ouvre deux coffres du même type est égale à 3/10.

3) Tim ouvre deux coffres du même type. Quelle est probabilité que ces coffres soient du type rare ?

4) On prend au hasard n matchs où Tim a ouvert deux coffres d’affilée, en supposant que ces matchs sont pris de manière identique et indépendante (à chaque fois, on ignore où Tim se situe dans le cycle).

On appelle X la variable aléatoire qui donne le nombre de fois où Tim a ouvert deux coffres du même type suite à ces n matchs.

a) Déterminer la loi de probabilité suivie par X.
b) Pour n = 10, déterminer la probabilité qu’il ait ouvert exactement 5 fois deux coffres du même type (arrondir le résultat au millième près) .
c) Pour quelle valeur minimale de n la probabilité pour Tim d’ouvrir au moins une fois deux coffres du même type est-elle supérieure à 99% ? Justifier la réponse par le calcul.

5) Au bout de combien de matchs indépendants où Tim ouvre deux coffres d’affilée, son espérance d’obtenir un coffre de type épique est-elle au moins égale à 1 ?

Annexe