Niveau : Cinquième
Chapitres : Calcul littéral
Inédit, publié le 03/09/2022

Diffusée sur le créneau de midi depuis plus de 15 ans, à la même heure que l’émission concurrente « Les douze coups de midi », l’émission « Tout le monde veut prendre sa place » (en abrégé : « TLMVPSP ») est un jeu télévisé basé sur un principe simple de questions-réponses. Le but pour les candidats est de déloger le ou la champion(ne), qui revient dans l’émission tant qu’il/elle n’a pas perdu : c’est ainsi que la plus grande championne de l’histoire de l’émission, Marie-Christine, est revenue pas moins de 217 fois !
Le jeu se déroule sur plusieurs manches, dans lesquelles les candidats répondent à diverses questions avec 3 modes possibles (au choix ou non du candidat, selon la situation) :
– Le mode « Duo » : il y a deux choix de réponses. Choisir la bonne réponse rapporte 1 point.
– Le mode « Carré » : il y a quatre choix de réponses. Choisir la bonne réponse rapporte 3 points.
– Le mode « Cash » : sans choix de réponses possibles, il faut donner la bonne réponse qui rapporte 5 points.
1) Dans la première manche du jeu, « Les Qualifs », les joueurs répondent à 4 questions. Pour l’une d’entre elles, ils doivent répondre en mode « Carré ». Pour les trois autres, les joueurs choisissent leur mode de réponse.
Quel est le nombre de points maximum qu’un joueur peut marquer dans cette première manche ?
2) Dans la seconde manche, « La Compet’ », les joueurs répondent au total à 9 questions : 3 en mode « Duo », 3 en mode « Carré », 3 en mode « Cash ».
Considérons Matilda, une candidate, qui répond de manière correcte dans cette manche à x questions en mode « Duo », y questions en mode « Carré » et z questions en mode « Cash ».
a) Quelle est la valeur maximale de la somme x + y + z ?
b) Donner, avec une expression qui contient les lettres x, y, z, le score de Matilda dans cette manche.
c) Calculer alors le score de Matilda qui est tel que x = 2, y = 3 et z = 2.
3) Trouver une autre manière de faire le même score que celui réalisé par Matilda, mais avec un triplet de valeurs x, y, z différent.
4) Dans la dernière manche, « Le Défi », un(e) seul(e) candidat « challenger » affronte un(e) champion(ne) en place. Chacun des deux répond tour à tour à une série de 6 questions. Les candidats répondent à chaque question avec le mode qu’ils souhaitent.
Supposons que Matilda décide de répondre en mode « Carré » à toutes les questions, et qu’elle réponde correctement à t questions. Le champion en place, qui ne répond à aucune question en mode « Duo », répond correctement à m questions en mode « Carré » et n questions en mode « Cash ».
a) Remplir le tableau ci-dessous, qui donne le score du champion en fonction des nombres m et n.
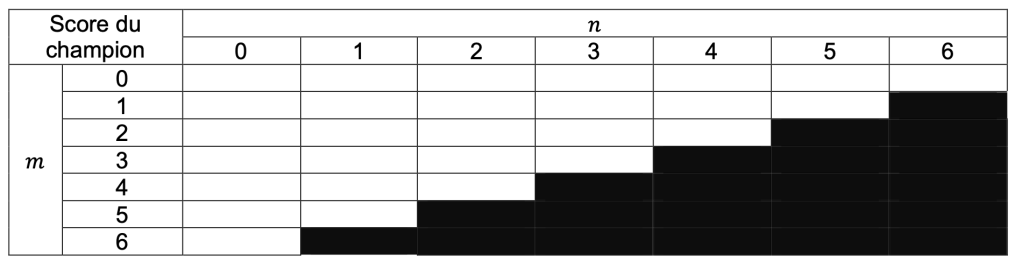
b) Matilda et le champion finissent par obtenir le même score. Exprimer avec une égalité contenant les lettres m, n et t ce fait de jeu.
c) Le champion a répondu correctement à au moins une question en mode « Carré » et au moins une question en mode « Cash ». Trouver alors le seul triplet de valeurs m, n et t qui permet de rendre l’égalité de la question précédente vraie.
Encore une super idée ! Merci !
J’aimeJ’aime