Niveaux : Terminale (Spécialité Maths)
Chapitres : Fonctions exponentielle et logarithme, Convexité, Probabilités
Inédit, publié le 10/12/2023

Qu’est-ce qui lie le monde des échecs au football américain, au billard ou à des jeux vidéos comme PUBG ou Overwatch? Le classement Elo. Nommé d’après le physicien qui l’a inventé, Arpad Elo, ce système permet d’estimer directement, d’après le nombre de points de deux joueurs obtenus dans ce classement, la probabilité qu’a chaque joueur de gagner contre un autre. Ce système se révèle très performant pour estimer sur le long terme le niveau d’un joueur : on se propose dans ce problème d’en regarder les aspects principaux.
Pour comprendre le système, considérons Armand et Béatrice, un lycéen et une lycéenne qui jouent très régulièrement aux échecs, et dont les nombres de points dans le classement Elo sont respectivement désignés par RA et RB. La probabilité pour Armand de battre Béatrice, notée pA/B, est alors donnée par :
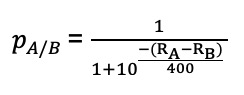
On admet que ce système ne considère pas de probabilité pour un match nul.
1) a) Prouver que la probabilité pB/A pour Béatrice de battre Armand est bien donnée par la formule :
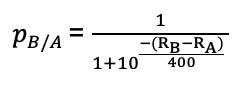
b) On donne RA = 1 530 et RB = 1 210. Calculer pA/B et en déduire pB/A (arrondir au centième près).
2) Pour x ∈ ℝ, on pose alors :
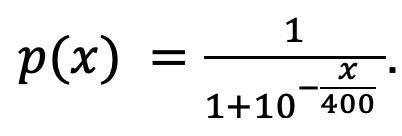
x désigne donc la différence de points relative qu’a un(e) joueur(se) avec un(e) autre (une différence positive indiquant qu’il ou elle est normalement meilleur(e) que l’autre) et p(x) la probabilité qu’il ou elle a de battre cet(te) autre joueur(se).
a) Déterminer les limites de p en +∞ et –∞, et calculer p(0). Vérifier la cohérence des résultats dans le contexte du classement Elo.
b) Calculer p'(x), et en déduire les variations de p sur ℝ.
3) a) On pose s(x) = p(x) – 1/2. Montrer que s est une fonction impaire.
b) Justifier que la dérivée seconde de s est également impaire.
c) Calculer la dérivée seconde de s et montrer qu‘elle est négative pour x ∈ ℝ+.
d) En déduire l’étude de la convexité de p sur ℝ.
4) Calculer la plus petite valeur entière de x pour laquelle p(x) > 0,9. Interpréter le résultat dans le contexte du classement Elo.
5) Après chaque match, les nombres de points Elo respectifs des deux joueurs ou joueuses qui se sont affronté(e)s évoluent. Quand un(e) joueur(se) affronte un(e) autre et qu’il ou elle a une différence relative de x points avec son adversaire, son nouveau score R’ est calculé à partir de son score R initial par la formule :
R’ = R + K(W – p(x))
Le coefficient K est nommé « le coefficient de développement » et dépend de plusieurs facteurs. Pour la plupart des joueurs(ses) amateurs réguliers aux échecs, il est égal à 20.
La valeur de W dépend du résultat du match : il vaut 1 pour une victoire, 0,5 pour un match nul et 0 pour une défaite.
a) Prouver que si deux joueurs(ses) avec le même K s’affrontent, le nombre de points gagnés par le ou la joueur(se) gagnant(e) est toujours égal au nombre de points perdus par le ou la joueur(se) perdant(e).
b) En cas de match nul, à quelle condition les nombres de points des deux joueurs(ses) n’évoluent-ils pas ?
c) Béatrice bat Armand. Calculer le nouveau nombre de points R’A et R’B après ce match, en prenant K = 20 (arrondir à l’entier près).