Niveaux : Terminale (Spécialité Maths)
Chapitres : Fonctions trigonométriques, Convexité, Continuité
Inédit, publié le 21/07/2025
Très fréquemment présent dans les fêtes foraines ou dans les parcs aquatiques, le toboggan vague géant ravit toujours les plus jeunes (et un peu moins les grands lycéens…) qui se laissent glisser pour quelques secondes de plaisir. Avec plusieurs pistes parallèles, le toboggan présente une forme de vague descendante (voir image ci-contre) qui va être l’objet de notre étude.

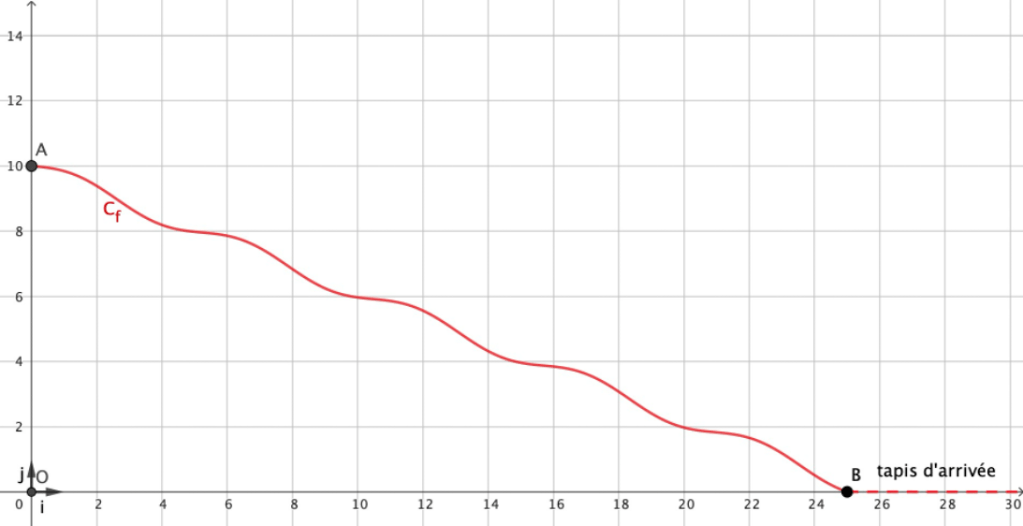
On sait que ce toboggan part de 10 mètres de hauteur et a une longueur de piste d’environ 27 mètres(1). Pour modéliser la courbe de la vague, on va utiliser un repère orthonormé (O, i, j) où l’unité de longueur est le mètre. On place alors le départ du toboggan au point A(0 ; 10) et son arrivée au point B(25 ; 0), où commence le tapis d’arrivée horizontal. On admet alors que la courbe du toboggan, sur l’intervalle [0;25] peut être modélisée par la courbe Cf représentative d’une fonction f d’expression :
f(x) = 10 – 0,39x + 0,25sin(1,2x)
On admettra que f est définie sur [0;25] et dérivable deux fois sur [0;25[. La courbe Cf est dessinée dans le repère en Annexe.
1) En utilisant les points A et B (on admet que f(25)≈0), calculer la pente moyenne du toboggan en degrés.
2) a) Calculer la dérivée f’ de la fonction f.
b) Justifier que : ∀ x ∈ [0;25[, f'(x)<0.
c) Montrer que f'(x) est une fonction périodique, dont on déterminera la plus petite période.
3) a) Calculer la dérivée seconde f’ ‘ de la fonction f.
b) Déterminer, en le justifiant, les abscisses de tous les points d’inflexion de la courbe Cf sur l’intervalle [0;25[.
4) a) En quelle(s) valeur(s) de x la pente de la courbe Cf , en valeur absolue, est-elle maximale?
b) Calculer en degrés l’angle de la pente de la courbe pour ces valeurs.
5) Si on prolongeait f pour x>25 en la définissant telle que f(x)=25 pour tout x>25, que pourrait-on dire de la continuité de f’ et f’ ‘ en x=25 ?
Annexe
Activité de prolongement : nous vous invitons à découvrir comment l’expression de la fonction f a été déterminée, en partant d’une expression de la forme f(x) = 10 – ax +bsin(cx) où a, b et c sont trois paramètres variables. L’activité permet de visionner l’influence de chacun des trois paramètres sur la forme de la courbe. On pourra cliquer ici : https://www.geogebra.org/m/zsxatgzs.
(1) Remerciements aux propriétaires de l’attraction « Toboggan Wave » présente durant les Fêtes de la Madeleine pour les quelques renseignements techniques fournis.