Problème 543 – Arsène Lupin et la faille du musée

Niveaux : Troisième
Chapitres : Théorème de Thalès, Trigonométrie, Proportionnalité (Distance/Vitesse/Temps)
Inédit, publié le 03/07/2025

          Personnage célèbre de la littérature française récemment remis au goût du jour par une série avec l’acteur Omar Sy, Arsène Lupin est connu comme étant le plus fameux des gentlemen cambrioleurs. Son intelligence lui permet de réaliser les tours les plus astucieux, avec une préparation toujours très minutieuse de ses vols. Tout justement dans ce problème, nous allons essayer de voir comment il prépare un nouveau vol de collier après avoir détecté une faille dans un musée. 

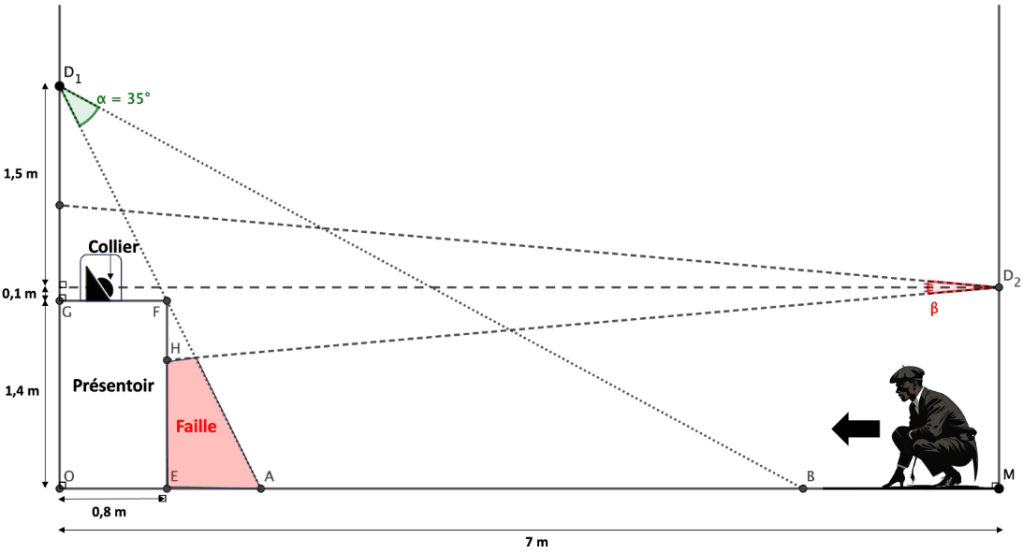
        Arsène Lupin a étudié le système de détection qui se trouve autour du collier qu’il souhaite voler, en faisant un schéma en Annexe. Dans une salle dont la largeur OM est égale à 7 mètres, le collier est posé sur un présentoir assimilable à un rectangle OEFG de largeur 0,8 m et de hauteur 1,4 m. Deux systèmes protègent le collier : le premier est une caméra, fixée en D₁ à 3 mètres de hauteur et qui voit tout ce qui se trouve dans le triangle D₁AB où A et B sont deux points du sol tels que AD₁B = α = 35°. Le second est un détecteur fixé en D₂, de l’autre côté de la salle, en étant exactement à hauteur du cœur du collier, à 10 cm au-dessus du présentoir. Il voit tout ce qui se passe dans la salle sous un angle β, dont la bissectrice, horizontale, passe par le cœur du collier. 

         Arsène Lupin pense avoir détecté une faille (qui ne serait que le début du plan !): en partant de l’autre côté de la salle accroupi près du point M, s’il arrive à distraire, avec l’aide d’un ami, le gardien qui contrôle la caméra D₁, il pourrait peut-être atteindre le présentoir près du point E et se cacher pour n’être vu ni par la caméra, ni par le détecteur, dans la « faille » visible en Annexe. Mais tout dépend de l’angle β du détecteur, qu’il ne connaît pas !

Dans tout le problème, on arrondira les résultats obtenus au centième près.

1) Calculer la distance OA.

2) a) Calculer la mesure de l’angle OD₁B.
b) En déduire la distance OB, puis AB.

3) Arsène Lupin estime que son ami peut distraire le gardien contrôlant la caméra D₁ uniquement pendant 3 secondes. 

A quelle vitesse minimale, en m/s, Arsène Lupin doit-il traverser la distance AB pour qu’il ne soit pas vu par la caméra?

4) Quand Arsène Lupin s’accroupit, sa tête atteint une hauteur de 0,8 m. Cela veut dire que pour qu’il ne soit pas vu par le détecteur fixé en D₂, l’angle β de détection doit être au maximum tel que la distance verticale EH, non détectable au niveau du présentoir, doit être au minimum de 0,8 m.  

Déterminer quelle est la valeur maximale de β qui permettrait à Arsène Lupin d’envisager ce vol en exploitant cette faille. 

Annexe