Niveaux : Seconde
Chapitres : Échantillonnage, Algorithmique (Python)
Première distribution (en activité en groupes) le 12/06/2025
Remarque : pour la rendre plus concrète, l’activité a été déclinée la première fois avec de vrais paquets.

Ils ressemblent à des M&M’s… mais ils n’en sont pas. Les Skittles, reconnaissables à leur fameuse lettre S imprimée sur le bonbon sont ces petites gommes de fruits enrobées avec des goûts différents. Bien que les années aient permis aux Skittles de se décliner en différents goûts, on trouve encore aujourd’hui principalement dans des paquets de Skittles 5 couleurs correspondant à 5 goûts : rouge (fraise), vert (pomme verte), jaune (citron), violet (raisin) et orange (orange). Sont-ils toujours également répartis comme l’affirme la société qui les produit ?
1) a) Quelle est, en théorie, la proportion p de chaque couleur de Skittles ?
b) A combien de Skittles cela correspond-t-il dans un paquet de 34 Skittles ?
c) En déduire qu’il n’est pas possible d’avoir une égalité parfaite des nombres de Skittles de chaque couleur dans un paquet.
2) A l’aide d’un programme Python, on va modéliser la production d’un paquet de 34 Skittles, en nous concentrant uniquement sur la couleur rouge.
On imagine que pour remplir le paquet, l’usine dépose un à un, de manière totalement aléatoire, chaque Skittle en le choisissant parmi les 5 couleurs, sachant que chaque couleur a la même proportion p d’être choisie.
Compléter le programme de la fonction skittles_rouges() ci-dessous pour qu’elle simule le nombre de Skittles de couleur rouge présents dans un paquet de 34 Skittles pris au hasard dans la production.
Remarque : la dernière ligne, qui affiche le résultat, ne fait pas partie de la fonction.

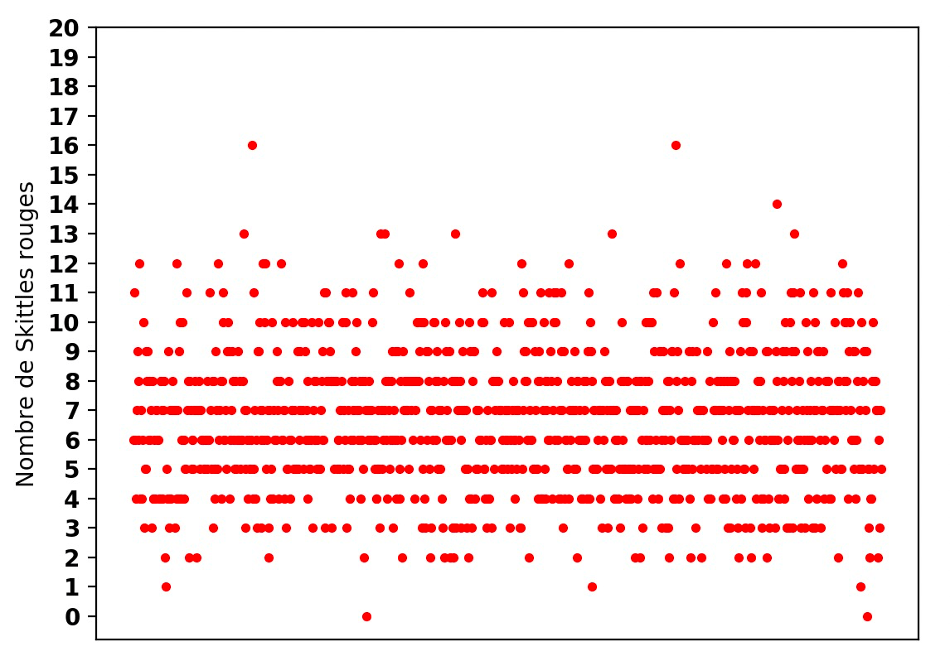
3) En utilisant la fonction skittles_rouges(), on a tracé graphiquement (en Annexe) le nombre de Skittles rouges présents dans 1000 paquets différents de 34 Skittles (chaque point représentant un paquet).
Confirmer d’après le graphique que le nombre moyen de Skittles rouges correspond approximativement à la valeur trouvée à la question 1.b).
Question supplémentaire pour ceux qui voudraient progresser davantage en Python : retrouver le programme qui a permis de tracer le graphique en Annexe.
4) a) Peut-on affirmer, d’après le graphique en Annexe, qu’au moins 95% des 1000 paquets produits semblent avoir une proportion de Skittles rouges dans l’intervalle de fluctuation [p – 1/√34; p + 1/√34] ?
b) On voit sur le graphique en Annexe que deux paquets n’ont aucun Skittle rouge, quand deux autres ont seize Skittles rouges. Si cette situation se retrouvait dans une usine, le fabricant devrait-il revoir ses méthodes de production ?
Annexe