Niveaux : Cinquième
Chapitres : Symétries
Inédit, publié le 22/04/2025

Revenir dans les souvenirs de l’école primaire avec le pliage d’une cocotte en papier (ou salière ? ou pouce-pouce ?…) : c’est ce que nous vous proposons de faire à travers ce problème ! N’avez-vous jamais joué le « diseur de bon aventure » en proposant à vos ami(e)s d’ouvrir une des huit cases mystères ? Si cela n’a jamais été le cas, ou si vous avez besoin d’un petit rappel, construisez votre cocotte (lien : https://ladigitale.dev/digiview/#/v/6806b4048acfb). Cela vous sera très utile pour pouvoir jouer … mais surtout, ici, pour y voir les effets de symétries.
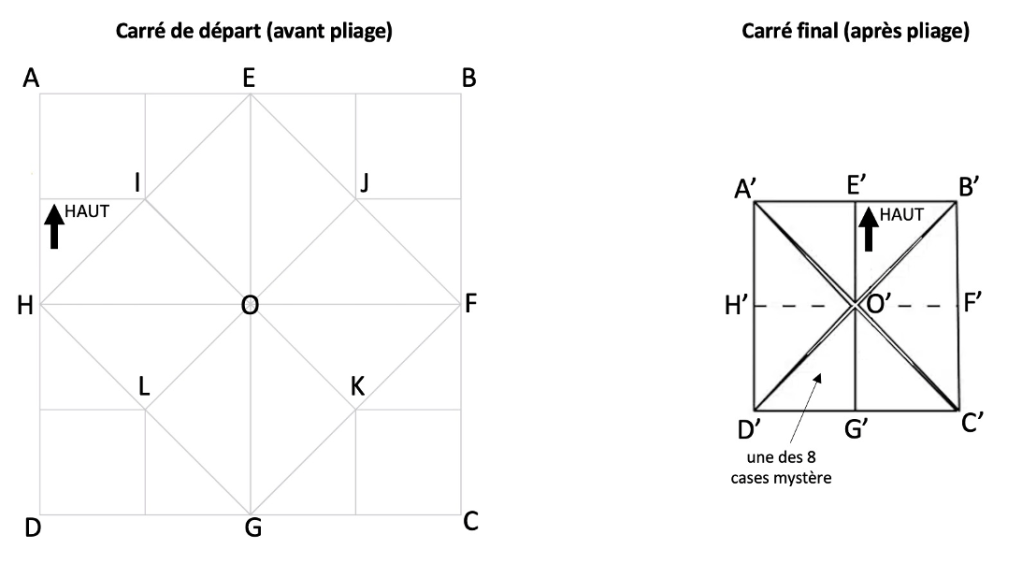
En effet, nous allons ici nous interroger sur les liens qui mènent du carré de départ au carré final – qui est celui qui se forme après deux séquences de plis, et à partir duquel on voit se former les 8 cases mystères. Ces deux carrés sont visibles en Annexe. Pour ce problème on a nommé ABCD le carré de départ (pas encore plié), avec son centre O, les milieux des côtés E, F, G et H, puis I, J, K, L les milieux des quatre « quarts de carré ». On a placé sur ce carré une flèche noire nommée « haut » : quand on forme après pliage le carré final, nommé A’B’C’D’ avec un centre O’, on s’assure ainsi, en tournant si nécessaire ce carré, que cette flèche reste bien orientée vers le « haut ».
1) a) A l’aide de votre cocotte, déterminer quels sont les points du carré de départ qui se retrouvent respectivement sur chacun des points A’, B’, C’, D’.
b) Quels sont de même les points du carré de départ qui se rejoignent au point O’ ?
2) a) Tracer précisément en Annexe, sur le carré initial, la flèche « a », symétrique de la flèche « haut » par rapport à la droite (HF).
Remarque : il n’est pas demandé de tracer le symétrique du mot « haut ».
b) Que devient alors la flèche « a » par rapport à la flèche « haut » sur le carré final ?
Indication : on utilisera dans la réponse la tournure : « elle est le symétrique de… par rapport à …»
3) Répéter les mêmes étapes que pour la question 2) pour une flèche « b », symétrique de la flèche « haut » par rapport au point O.
4) a) Tracer en Annexe, sur le carré final, la flèche « c », symétrique de la flèche « haut » par rapport à la diagonale (B’D’).
b) Indiquer à l’aide d’une symétrie comment la flèche « c » pourrait-être construite pareillement sur le carré de départ.
5) a) En Annexe, sur le carré final, tracer le carré E’F’G’H’ puis colorier son intérieur.
b) Colorier alors de la même couleur, sur le carré initial de l’Annexe, les différentes parties qui permettent de reconstituer E’F’G’H’ quand le papier est plié.
c) Désigner par le numéro « 1 » sur le carré de départ la partie coloriée qui touche la flèche « haut », puis numéroter successivement toutes les autres parties coloriées (« 2 », « 3 », « 4 » etc…) en tournant dans le sens des aiguilles d’une montre. Indiquer alors si la partie « 1 » peut ou non être reliée à chacune des autres parties par une symétrie axiale ou centrale (quand c’est possible, indiquer la droite ou le point de la symétrie).
Annexe