Problème 526 – Derrière les portes de la serre de Doors

Niveaux : 2 versions : Seconde/Première (Spécialité Maths)
Chapitres : Probabilités
Fait en collaboration avec Jimmy Donnelly, élève de 1^ère du lycée Gaston Crampe d’Aire-sur-l’Adour
Première distribution (en exercice en groupe) le 16 Avril 2025

            Entre escape game et film d’horreur, le jeu Doors, développé dans l’univers de Roblox, est un jeu sorti en 2022 dont l’objectif est de pouvoir traverser 100 portes d’un hôtel en restant vivant. L’originalité du jeu repose sur le fait que chaque nouvelle tentative est différente, puisque la manière dont les salles et les monstres sont répartis change à chaque tentative. Dans ce problème, nous allons nous intéresser aux probabilités de rencontrer certains de ces monstres, à la suite ou en même temps. Ceux qui ne connaissent pas Doors n’ont pas besoin d’y jouer pour résoudre le problème (mais rien ne vous empêche d’essayer si vous avez un compte Roblox…).

            On dénombre dans ce jeu 21 monstres ou « entités », dont les probabilités d’apparition sont expliquées dans une vidéo Youtube (en anglais, en cliquant ici). On y comprend alors que ces probabilités peuvent dépendre de plusieurs facteurs, notamment le fait que certains monstres n’apparaissent qu’après un certain nombre de portes franchies. Ici, plus particulièrement, nous allons nous intéresser à ces monstres qui apparaissent dans la fameuse « serre », située entre les portes 90 à 99. 

Les deux problèmes sont strictement indépendants.

Problème Niveau Seconde

            On s’intéresse aux monstres nommés « a-60 » et « a-90 », et notamment aux probabilités de les rencontrer juste après avoir ouvert une porte dans la serre.

          On appelle A l’évènement : « rencontrer a-60 juste derrière une porte ouverte dans la serre» et B l’évènement « rencontrer a-90 juste derrière une porte ouverte dans la serre ». Il est tout à fait possible de rencontrer les deux monstres en même temps derrière une même porte.

La vidéo indique alors que : p(A)=1/10 ; p(B)=1/20 et p(A∩B)=1/30.

Toutes les probabilités demandées ci-dessous concernent uniquement un évènement se produisant juste derrière une porte ouverte dans la serre (on ne le précisera donc plus).

1) Quelle est la probabilité de ne pas tomber sur a-60 ?

2) Expliquer par une phrase ce qu’est l’évènement A∪B et en calculer la probabilité.

3) a) A l’aide de A et B, écrire de deux manières différentes l’évènement : « ne tomber sur aucun des deux monstres ».
b) Calculer la probabilité cet évènement. 

4) a) Calculer, en justifiant, la probabilité de ne tomber que sur a-60 sans tomber sur a-90.
b) Même question pour a-90 sans a-60.

5) Un autre fameux monstre, Eyes, a une probabilité d’apparition derrière une porte dans la serre de 1/5. Ce monstre ne peut apparaître ni avec a-60, ni avec a-90 (et encore moins avec les deux !).

On appelle C l’évènement : « rencontrer Eyes après avoir ouvert une porte dans la serre ».

a) Dessiner un diagramme de Venn faisant apparaître les évènements A, B et C, ainsi que les probabilités de toutes les zones séparées visibles sur le diagramme. 

b) Quelle est la probabilité de l’évènement A∪B∪C?

Problème Niveau Première

            On étudie la présence de deux monstres, Ambush et Rush, qui apparaissent de manière plus fréquente dans la serre que dans les niveaux précédents. On va considérer l’apparition de ces monstres, qui ne peut pas être simultanée, derrière chacune des portes 90+n, n allant donc de 0 à 9.

En nous appuyant sur les données de la vidéo, on suppose que :

• Si aucun des deux monstres n’est apparu derrière la porte 90+n, la probabilité d’apparition de Rush derrière la porte 90+n+1 est 1/5, alors que celle d’Ambush est 1/20.
• Si Rush est apparu derrière la porte 90+n, il n’a aucune chance d’apparaître derrière la porte 90+n+1, alors que Ambush a une chance d’apparition de 1/5.
• A l’inverse, si Ambush est apparu derrière la porte 90+n, il n’a aucune chance d’apparaître derrière la porte 90+n+1, alors que Rush a une chance d’apparition de 1/20.

On nomme les évènements :

A_n: « Ambush apparaît derrière la porte 90+n ». On note p(A_n) = a_n.
R_n: « Rush apparaît derrière la porte 90+n » On note p(R_n) = r_n.
V_n: « Aucun des deux monstres n’apparaît derrière la porte 90+n».

On suppose qu’aucun des deux monstres n’est derrière la porte 90. On a donc a₀ = r₀ = 0.

Dans tout le problème, on arrondira les résultats obtenus au millième près.

1) Déterminer la probabilité qu’aucun des deux monstres n’apparaisse derrière la porte 91.

2) Calculer p(A₂) et p(R₂).

3) En vous appuyant sur l’énoncé, compléter l’arbre de probabilités ci-dessous.

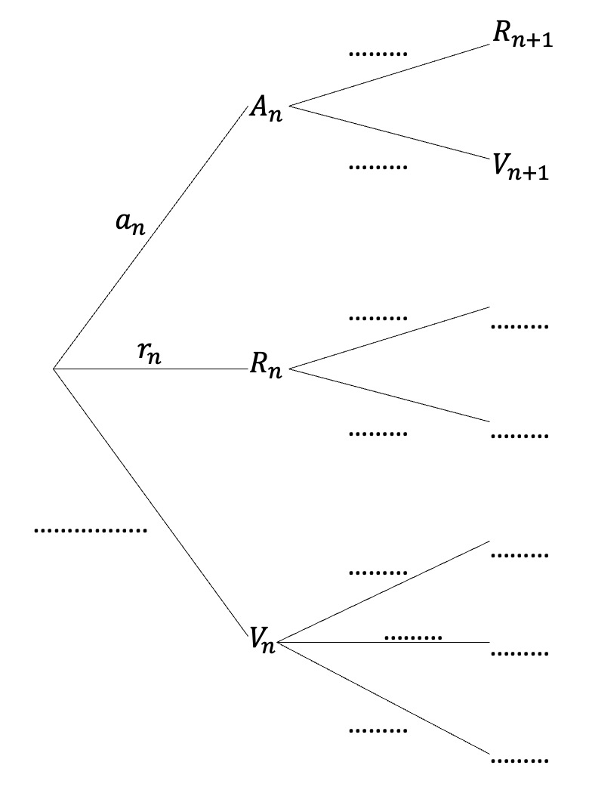
4) Montrer que a_n+1 = 1/5*(1 – a_n) et que r_n+1 = 1/20*(1 – r_n)

5) On pose la suite (u_n) définie pour tout entier n entre 0 et 9 par u_n = a_n – 1/6 .
a) Montrer que (u_n) est une suite géométrique dont on déterminera le premier terme et la raison.
b) En déduire une expression de u_n puis de a_n en fonction de n.
c) En répétant le même procédé avec la suite (v_n) définie pour tout entier n entre 0 et 9 par 
v_n = r_n – 1/21, déterminer une expression de r_n en fonction de n.

6) En déduire les probabilités respectives que Ambush et Rush apparaissent derrière la porte 99.