Niveaux : Quatrième (ou début de Troisième)
Chapitres : Volumes, Grandeurs-produit
Inédit, publié le 13/04/2025

Dans l’ère de l’électronique que nous traversons actuellement, les piles jouent un rôle central. Petites batteries qui font fonctionner les appareils, elles sont aujourd’hui de toutes tailles et de toutes formes, en fonction de l’usage. On peut difficilement s’en passer, mais très souvent, on n’a pas chez soi la pile à la dimension voulue : qui ne s’est jamais retrouvé à chercher une « AAA » quand on n’a que des « AA » ? Dans ce problème, on va s’intéresser à celles qui sont les plus utilisées dans notre quotidien, et faire quelques calculs autour de leur volume et de leur capacité.
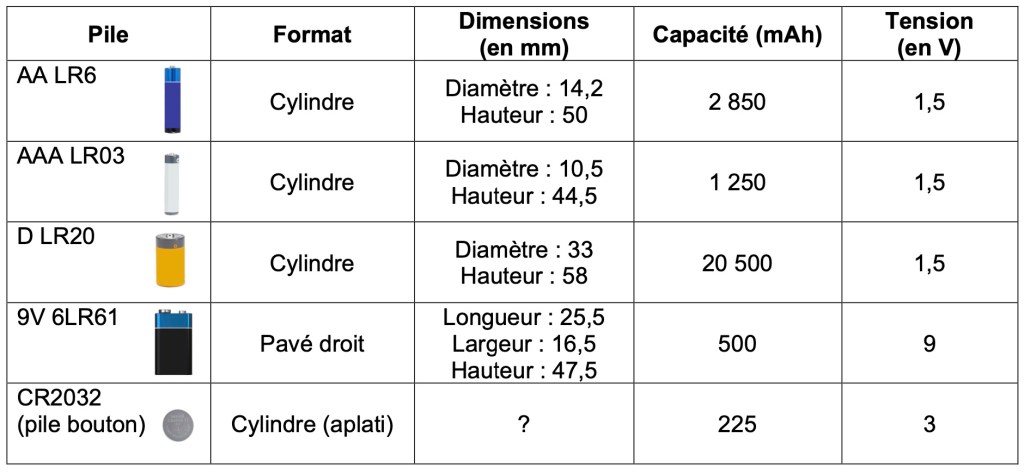
Parmi les modèles les plus utilisés, on trouve fréquemment les piles AA LR6, AAA LR03, C LR14, 9V 6LR61, CR2032 dont on a résumé les caractéristiques principales (dimensions, capacité, tension) dans le tableau en Annexe. Remarquons que quatre d’entre elles ont une forme cylindrique, et qu’une est en forme de pavé droit : on admettra, pour ce problème, notamment pour les calculs de volumes, que ces formes sont exactes – et donc qu’on ignorera par exemple les bouts des piles ou les bords arrondis.
Dans tout le problème, on arrondira les résultats obtenus à l’entier près.
1) Calculer le volume, en mm3, des piles AAA LR03, D LR 20 et 9V 6LR61.
2) Le volume d’une pile bouton CR2032 est d’environ 1 cm3, avec une épaisseur de 3,2 mm. Quel est son diamètre en mm ? Justifier les calculs.
3) John, un collégien, veut comparer le volume des piles AA et AAA.
Pensant être malin, il se contente de faire le calcul suivant : (50÷44,5) x (14,2÷10,5) ≈ 1,5. Il en déduit que le volume de la pile AA est environ 1,5 fois plus grand que celui de la pile AAA.
Expliquer le raisonnement de John quand il fait ce calcul, et sans calculer le volume de la pile AA, expliquer pourquoi ce raisonnement est incorrect.
4) On rappelle que la capacité (ou charge), exprimée en mAh, est une grandeur-produit, issue du calcul :
Capacité (en mAh) = Intensité (en mA) x temps (en heures)
John insère une pile neuve AAA dans sa calculatrice de collège. Il utilise celle-ci en moyenne chaque jour 15 minutes par jour en état inoccupé (à une intensité de 0,8 mA) et 5 minutes en état de calcul (à une intensité de 17 mA).
Elle indique qu’en théorie, une pile ayant une capacité de 1 mAh peut faire fonctionner un appareil pendant 1 heure si l’intensité est de 1 mA.
Combien de jours en théorie John pourra-t-il utiliser sa calculatrice avant de devoir changer la pile ?
5) « Plus une pile a un volume important, plus sa capacité est importante » : montrer sans calculs additionnels que cette affirmation est incorrecte, et en déterminer une des raisons possibles.
Indication : quelles sont les données du tableau qui n’ont pas encore été utilisées jusqu’ici ?
Annexe