Niveaux : 1ère (Tronc commun)
Chapitres : Variations instantanées, Nombre dérivé
Première distribution (en devoir en groupes) le 24/03/2025
Note: un énoncé similaire, utilisé en sujet de secours, est disponible sur le problème 528 – Le pic de Pinterest.

En proposant dès 2009 une messagerie instantanée gratuite capable de supplanter le téléphone classique, WhatsApp s’est imposé en quelques années comme une des applications les plus populaires dans le monde. Devenue un réseau social, elle a dépassé en 2020 les 2 milliards d’utilisateurs … et ce nombre continue de grandir, même si la vitesse de croissance semble se tasser, comme nous allons le voir dans ce problème.
On se propose ainsi d’étudier la courbe du nombre d’utilisateurs de WhatsApp dans le monde depuis la création de l’application en 2009 : celle-ci est représentée sur le graphique en Annexe. Elle est la courbe représentative d’une fonction f. En abscisse, l’unité t représente le nombre de trimestres écoulés depuis la création du WhatsApp lors du 2ème trimestre de l’année 2009 (on écrira donc qu’à t = 0, on est au « Q2 2009 »). En ordonnée, l’unité est le nombre d’utilisateurs en millions. On pourrait donc écrire par exemple qu’à t = 12, donc au bout de 3 ans au Q2 2012, l’application comptait environ 100 millions d’utilisateurs.
1) a) Combien WhatsApp comptait-il d’utilisateurs à t = 25 (au Q3 2015) ?
b) Pour quelle valeur de t WhatsApp a-t-il dépassé les 1,5 milliards d’utilisateurs ? A quel trimestre cette valeur correspond-t-elle ?
2) a) Tracer en rouge sur le graphique en Annexe la droite sécante à la courbe reliant le point de la courbe d’abscisse t = 0 et celui d’abscisse t = 60.
b) A quoi correspond le coefficient directeur de cette sécante ? En quelle unité s’exprime-t-il ?
c) Déterminer graphiquement la valeur de ce coefficient directeur.
3) On a tracé sur le graphique en Annexe la tangente à la courbe au point A d’abscisse t = 50.
a) Déterminer graphiquement la valeur de f(50) et de f'(50).
b) En déduire l’équation de cette tangente.
4) a) Déterminer visuellement sur la courbe pour quelle valeur t0 la valeur de f‘ semble la plus élevée.
b) Que signifie alors ce moment t0 dans l’histoire de la croissance de WhatsApp ?
Remarque : pour répondre à cette question, on pourra utiliser le terme « vitesse ».
5) On voit que, sur les derniers trimestres, pour t ≥ 55, la croissance de WhatsApp commence à se tasser. Qu’en déduit-on sur l’évolution de f’ pour t ≥ 55?
Annexe
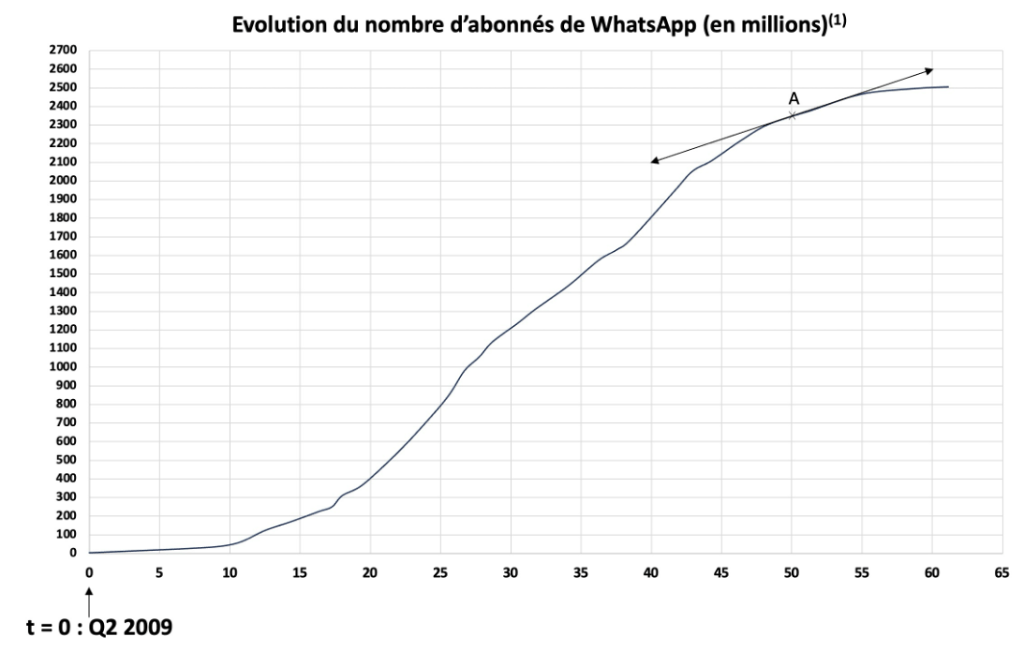
(1) Source : https://www.businessofapps.com/data/whatsapp-statistics/