Problème 488 – Les déplacements du damier

Niveaux : Seconde
Chapitres : Ensembles de nombres, Racines carrées
Inédit, publié le 30/09/2024

            Aussi classique que les échecs, le jeu de dames se joue sur un damier de 10 cases sur 10 cases, avec une alternance de cases blanches et noires. 20 pions blancs affrontent 20 pions noirs en se déplaçant uniquement de manière diagonale, d’une case noire à une autre. Si les pions simples ne peuvent se déplacer que d’une case, les dames, que l’on obtient en atteignant la ligne adverse la plus éloignée, peuvent, elles, se déplacer de plusieurs cases toujours le long d’une diagonale. Dans ce problème, nous nous intéressons à la nature des distances parcourues possibles. Il est inutile pour ce problème de savoir jouer aux dames…

            Considérons un damier dont le côté d’une case mesure x cm. Cette longueur est aussi celle qui sépare les milieux de deux cases adjacentes. Sur la figure en Annexe, on voit les déplacements possibles d’un pion simple et ceux d’une dame⁽¹⁾, qui vont uniquement du milieu d’une case à un autre. 

1) Exprimer en fonction de x la longueur en cm du déplacement d’un pion simple.

2) On suppose pour cette question que x = 1 cm.
a) Calculer la longueur, en cm, de la diagonale maximale théorique que peut faire une dame sur un damier, sachant qu’elle peut partir de n’importe quelle case noire du damier.

b) Exprimer le résultat obtenu sous les deux formes possibles : √a ou b√2, avec a et b entiers.

3) On suppose pour cette question uniquement que x est un entier.
a) Montrer que quel que soit son déplacement, la longueur du déplacement d’une dame en cm ne peut pas être un nombre décimal.

b) Montrer que quel que soit son déplacement, la longueur du déplacement d’une dame en cm ne peut pas être un nombre de la forme √n, avec n un nombre entier impair.

4) Montrer que si x est un nombre rationnel, alors la longueur du déplacement d’une dame en cm, quel que soit son déplacement, ne peut pas être un nombre rationnel.

5) Dessiner à taille réelle un quart de damier (5 cases x 5 cases) dont la longueur du côté d’une case soit égale à exactement 3√2/2 cm. Expliquer la démarche. 

Annexe⁽²⁾

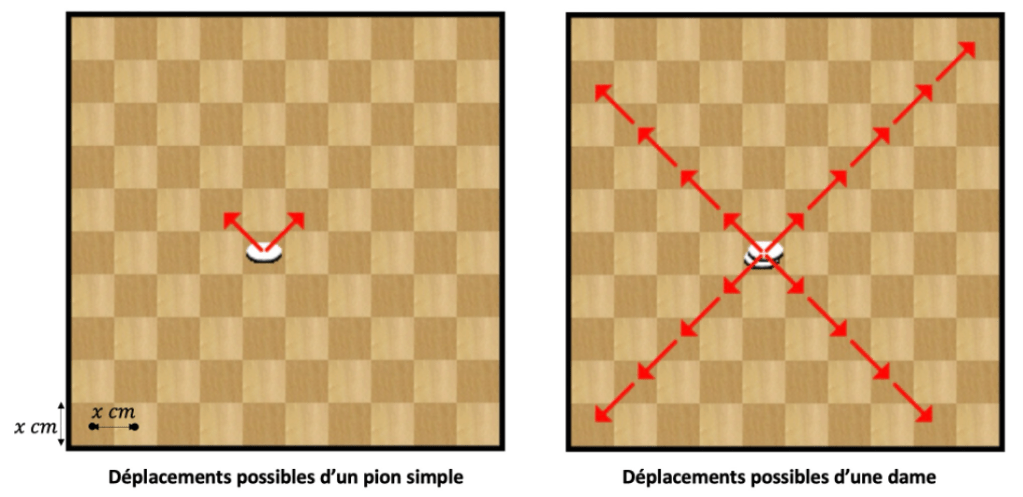
(1) Pour ceux qui savent jouer : on ignorera pour ce problème le fait de pouvoir sauter au-dessus d’un pion adverse pour le capturer, ou le fait que des enchaînements de diagonales sont possibles grâce aux captures multiples.
(2) Source images : http://www.ffjd.fr/Web/index.php?page=reglesdujeu