Problème 472 – Le jeu de l’oie en deux coups

Niveaux : Première (Spécialité Maths ou Tronc commun)
Chapitres : Probabilités
Inédit, publié le 02/08/2024

            Inventé à la fin du XVI^ème siècle, le jeu de l’oie fait partie de ces jeux traditionnels qui réunissent encore les familles (mais faites-vous partie de ceux qui savent y jouer ?). Les règles sont faciles à comprendre : partir de la case 0, lancer deux dés à six faces chacun à son tour, avancer du nombre de points affichés à chaque tour… et être le premier à arriver très exactement à la case numérotée 63. Bien sûr, un certain nombre de cases spéciales pimentent le jeu ; certaines permettent même de terminer le jeu extrêmement vite (ou alors de tout perdre !) : nous allons, dans ce problème, nous intéresser à ces cases.

            Par exemple, si un joueur ou une joueuse fait 9 au premier coup de dés avec un 4 et un 5, et uniquement à ce premier coup, il ou elle se téléporte automatiquement à la case 53. Cela veut notamment dire que si l’on fait ensuite 10 au second coup de dés (puisqu’il faut tomber pile sur la case 63), la partie est déjà terminée. Il n’y a pas d’autres moyens de gagner aussi vite…

1) Soit A l’évènement : « Faire apparaître un 4 et un 5 au premier coup de dés »
Soit B l’évènement : « Tirer un 10 au second coup de dés »

a) Calculer p(A) et p(B).

b) Remplir l’arbre de probabilité ci-dessous.

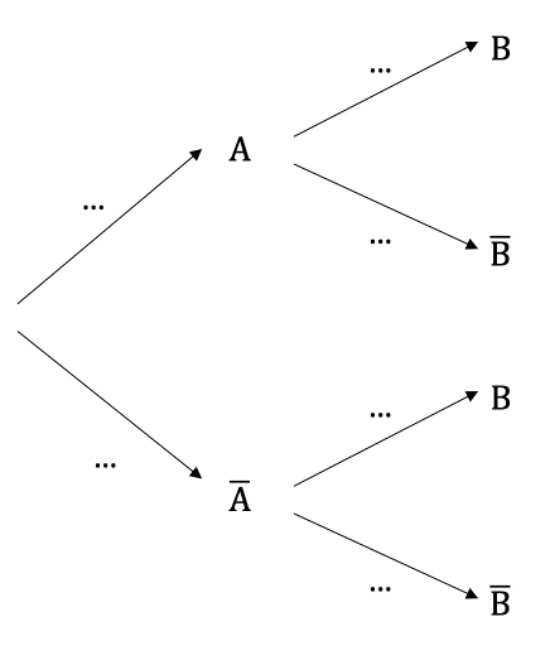
c) Quel est l’évènement qui indiquerait que le joueur ou la joueuse a gagné en deux coups de dés ? Quelle est sa probabilité ?

2) Les évènements A et B sont-ils indépendants ? Justifier la réponse.

3) On observe un joueur qui fait 10 au second coup de dés.
Quelle est la probabilité qu’il ait déjà gagné la partie ?

4) On considère l’évènement C : « le joueur ou la joueuse gagne au deuxième coup ».
a) B et C sont-ils les mêmes évènements ? Expliquer. 
b) Si C est réalisé, quelle est la probabilité que A ait été réalisé ?
c) Qu’en déduit-on sur l’indépendance des évènements A et C ?

5) Si un pion tombe sur la case 58, il tombe sur la case de la tête de mort et revient à la case départ. Il n’y a pas d’autres moyens de revenir à la case départ en deux coups de dés.

En deux coups de dés, y a-t-il plus de chances de gagner la partie ou plus de chances de revenir à la case départ ? Justifier la réponse.