Problème 453 – Couleurs et symétries à Jungle Speed

Niveaux : Cinquième
Chapitres : Symétries, Probabilités
Inédit, publié le 11/05/2024

        Le jeu Jungle Speed – où il faut attraper le totem quand deux cartes avec le même symbole apparaissent – est un grand classique : il a déjà plus de 30 ans ! Dans sa version de base (donc hors des extensions), il contient 80 cartes carrées: 72 cartes « standard », réparties en 18 symboles différents déclinés en 4 couleurs (bleu, jaune, rouge, vert), et 8 cartes avec des symboles spéciaux : 3 « flèches vers l’intérieur », 3 « flèches vers l’extérieur » et 2 « flèches de couleur ». Sans qu’il ne soit nécessaire de comprendre les règles du jeu, nous allons nous intéresser dans ce problème à toutes les symétries contenues dans les cartes, pour ensuite calculer quelques probabilités.

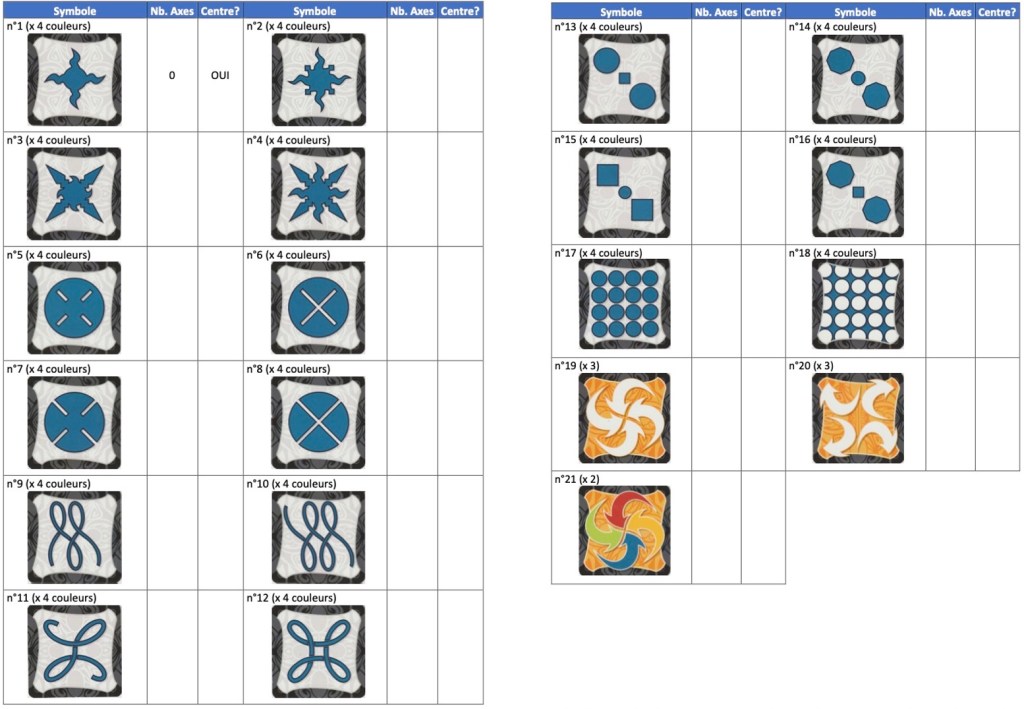
         On a repris en Annexe l’ensemble des symboles apparaissant dans le jeu en les numérotant, en ne prenant, pour les 18 premiers symboles, que ceux de couleur bleue. 

Dans tout le problème, on écrira les probabilités à calculer sous la forme d’une fraction simplifiée.

1) Remplir le tableau en Annexe en indiquant pour chaque symbole le nombre d’axes de symétrie, et si la figure contient ou pas un centre de symétrie (un exemple est donné pour le symbole n°1).

2) Adélaïde et Benoît font une partie avec un paquet complet de 80 cartes. Adélaïde fait apparaître une première carte. 

Combien d’issues différentes existe-t-il ? Ont-elles toutes la même probabilité ?

3) Quelle est la probabilité que la carte retournée par Adélaïde contienne:
a) Un symbole de couleur (uniquement) bleue ?
b) Un symbole n’admettant pas de centre de symétrie ?
c) Un symbole admettant au moins un axe de symétrie ?
d) Un cercle totalement complété (c’est-à-dire sans coupure) ?
e) Un symbole spécial ?
f) Du rouge ?

4) Proposer, pour le tirage effectuée par Adélaïde, un évènement dont la probabilité serait égale à 0.

5) Finalement, Adélaïde retourne une carte contenant le symbole n°1, et la laisse visible. Benoît retourne à son tour une autre carte. Quelle est la probabilité que la carte retournée soit aussi un symbole n°1 d’une autre couleur ?

Annexe