Problème 427 – Découper sur la fève

Niveau : Seconde
Chapitres : Fonctions, Variations et extremums, Trigonométrie, Probabilités
Inédit, publié le 21/01/2024

Dans ce problème, on se propose de reprendre une question très classique qui revient chaque année quand vient la période de la galette des rois : quelle est la probabilité, pour celui ou celle qui découpe la galette, de tomber sur la fève avec le couteau?

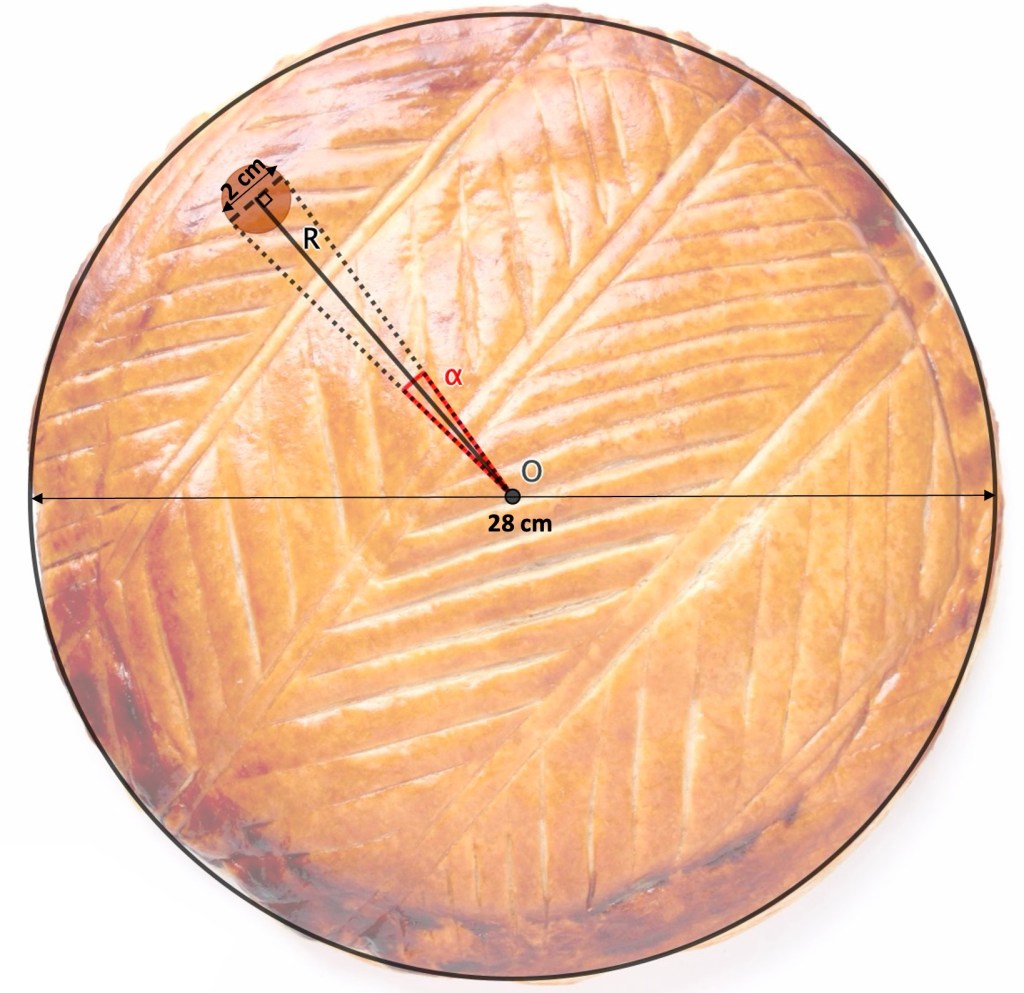
Pour répondre à cette question, on va reprendre un modèle très intéressant proposé par un contributeur sur le site « Zeste de savoir »⁽¹⁾. Le modèle considère une galette circulaire et, pour simplifier, une fève en forme de disque (voir figure en Annexe). Les bords de la fève créant avec le centre O de la galette un secteur d’angle α (exprimé en degrés), le modèle proposé explique que, si on coupe la galette en n parts égales, la probabilité de tomber sur la fève est égale à nα/360, sous réserve que nα < 360 (sinon quoi on est certain de tomber sur la fève).

Pour ce problème, on va prendre une galette pour 8 personnes dont le diamètre fait 28 cm. La fève est assimilée à un disque de diamètre 2 cm et son centre est placé à une distance R (en cm) du centre de la galette.

Dans tout le problème, les résultats obtenus seront, si nécessaire, arrondis au centième près.

1) Sachant que la fève doit être cachée dans la galette, donner la valeur maximale de R.

2) Montrer que si R > 0, on a : α = 2 x Arctan(1/R)

3) On considère uniquement pour cette question que R = 7.

a) Calculer α en degrés.
b) Pour quelle valeur minimale de n est-on certain de tomber sur la fève en découpant la galette?
c) Déterminer la probabilité de tomber sur la fève en découpant la galette quand n = 8.

4) On appelle p(R) la fonction qui à R associe la probabilité de tomber sur la fève en découpant la galette.

a) Donner l’expression complète de p en fonction de R.
b) En utilisant le fait que Arctan est une fonction strictement croissante, montrer que p(R) est strictement décroissante sur son intervalle de définition. Donner une interprétation de ce résultat.

5) On prend pour cette question n = 8.

a) Calculer la valeur minimale de p(R).
b) A l’aide de la calculatrice, trouver pour quelle valeur minimale de R (arrondie au centième) la probabilité de découper sur la fève est inférieure à la probabilité de l’éviter.

Annexe