Problème 423 – Suika Game, le jeu de la pastèque

Niveaux : 2 versions : Sixième/Cycle 3 et Première (Spécialité Maths)
Chapitres : Sixième/Cycle 3 : Cercles, Disques, Construction de triangles
Première : Vecteurs, Produit Scalaire, Configurations géométriques
Inédit, publié le 03/01/2024

            Sorti en 2021 au Japon, « Suika Game », le jeu de la pastèque, a commencé à déferler sur le monde en octobre 2023. Son succès a été quasi-immédiat. Le principe du jeu est un mélange entre « Tetris » – des fruits tombent et s’entassent – et « 2048 » – deux fruits similaires qui se touchent forment un fruit plus grand. Il y a 11 fruits classés par ordre de taille, et le but est d’obtenir 2 pastèques (le fruit le plus grand) qui se touchent. On ne saurait trop conseiller à ceux qui ne connaissent pas le jeu d’essayer au moins une fois, soit sur une application mobile, ou soit par exemple ici : https://www.smartjeux.com/jeu-de-la-pasteque (attention, c’est addictif !).

            On a rassemblé dans le tableau en Annexe 1 tous les fruits du jeu. Même s’ils ne sont pas tous absolument circulaires (par exemple la fraise ou le raisin), on admet pour ce problème qu’ils le sont et qu’ils ont un rayon, sachant que 1 unité de longueur est égale au rayon du plus petit fruit, c’est-à-dire la cerise. Ces rayons sont donnés dans le tableau en Annexe 1.

Les deux problèmes proposés sont totalement indépendants.

Toutes les longueurs seront calculées dans l’unité du problème. De même, l’unité d’aire est l’unité de longueur du problème multipliée par elle-même. Dans les deux cas, il ne sera pas nécessaire d’indiquer un symbole de longueur après les résultats trouvés.

On arrondira tous les résultats trouvés au centième près.

Niveau Sixième/Cycle 3

1) Calculer le périmètre d’une orange.

2) L’un de ces fruits a un périmètre environ égal à 30,2. Quel est ce fruit ? Justifier la réponse.

3) Calculer l’aire occupée par la pastèque. 

4) Quand deux pommes se touchent, elles se changent en une poire. Normalement, l’aire de la poire devrait être égale à la somme des aires de deux pommes. Or ce n’est visiblement pas le cas !

Calculer l’aire qui a été perdue quand deux pommes se sont transformées en poire.

5) a) On remarque que l’un des fruits a un rayon exactement deux fois supérieur à un autre. Quels sont ces deux fruits?

b) Marco affirme: « L’aire du plus grand de ces deux fruits vaut environ le double de l’aire de l’autre ». Nahia répond: « Non, ce n’est pas le double, c’est le quadruple ». Qui a raison? Justifier la réponse.

Question bonus (construction géométrique plutôt difficile !) :

Un ananas et un kaki sont posés en bas de l’écran et se touchent côte à côte.
Une orange vient se poser au-dessus des deux autres fruits et les touchent tous les deux.

En prenant pour échelle 1 cm = 1 unité, représenter la situation décrite ci-dessus à l’aide de trois cercles représentant les 3 fruits qui se touchent deux à deux (on représentera le bas de l’écran par une droite). On laissera clairement visibles les traits de construction.

Indication : deux cercles de rayons respectifs r et r’ qui se touchent sans se croiser sont tels que la distance entre leurs deux centres est égale à r + r’.

Niveau Première (Spécialité Maths)

Note: sur la version en ligne du problème, les vecteurs et angles sont écrits en gras italique.

On considère une situation où une pêche de centre A est tombée en bas de l’écran, suivie d’une orange de centre B qui touche la pêche. L’orange ne peut pas toucher le bas de l’écran car elle est bloquée à gauche par le mur, à une hauteur telle que son point le plus bas, S, à la verticale du point B, soit à une hauteur de 6 par rapport au bas de l’écran (voir figure en Annexe 2).

1) a) Calculer le produit scalaire BS.BA.

b) En déduire la mesure en degrés de l’angle SBA.

c) En déduire à quelle distance le point A se trouve du mur gauche.

2) Calculer la distance SA.

3) Une pomme de centre C tombe à son tour sur la pêche et l’orange, en étant tangents à ces deux derniers.

Placer avec précision le point C sur la figure en Annexe 2, et dessiner le cercle représentant la pomme.

4) Calculer en degrés une mesure de l’angle ACB.

5) On voudrait remplacer la pomme par un autre fruit de rayon r et de centre D tel que le triangle ABD soit rectangle en D. 

Déterminer la valeur de r, et choisir dans l’Annexe 1 le fruit qui se rapprochera le plus de la situation souhaitée.

Annexe 1

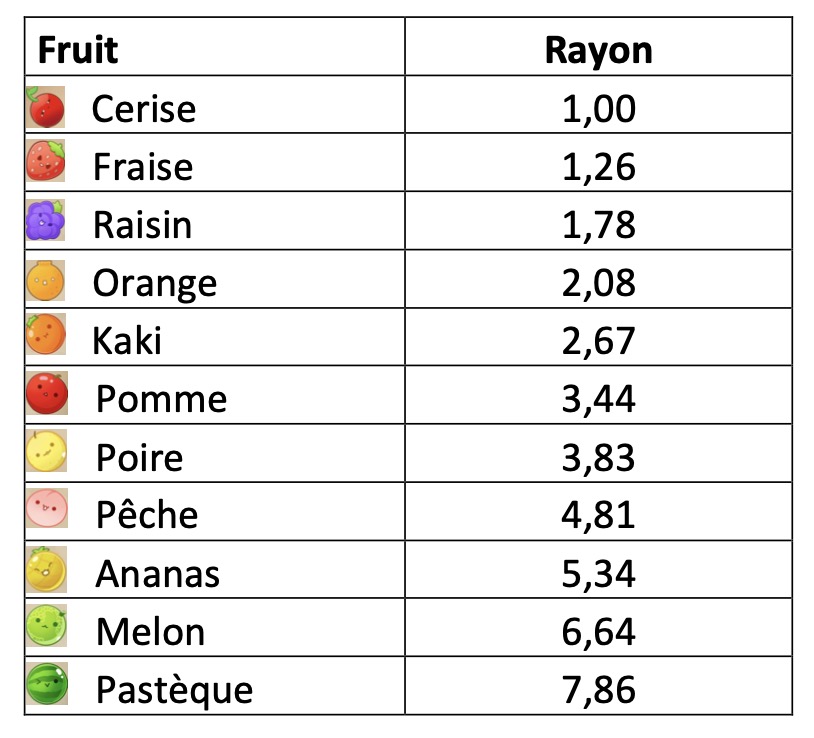
Annexe 2 (uniquement pour le problème pour la classe de Première)

Note : Remerciements pour l’idée du problème à mon neveu Aurélien…