Niveau : Troisième
Chapitres : Théorème de Thalès, Équations, Théorème de Pythagore, Volumes, Agrandissement/Réduction, Transformations géométriques (Homothéties)
Inédit, publié le 30/10/2023

S’il ne devait exister qu’un seul dessert emblématique du Portugal, ce serait lui : le pastel (au pluriel : pastéis). Souvent appelé « de Nata », même si les connaisseurs savent que l’original est celui « de Belém », ce petit flan est un véritable délice. Ceux qui, depuis toujours, le préparent en cuisine, connaissent l’importance de ses petites dimensions pour le garder croustillant et savoureux.
Pour mieux apprécier le pastel, on se propose dans ce problème de s’intéresser à sa forme. Pour en avoir une vision simplifiée, on modélise un pastel par une forme de cône renversé, tronqué horizontalement et parallèlement à la base du cône. La base du cône est un disque de diamètre 7,2 cm, la troncature se fait à 3 cm de la base, et la section plane formée par la troncature est un disque de diamètre 4 cm.
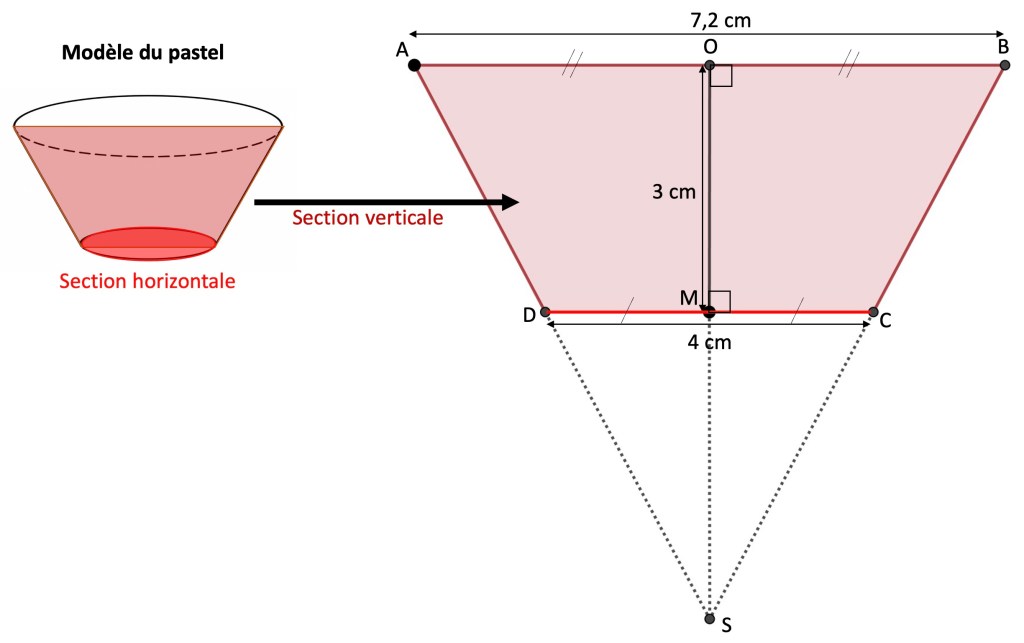
On représente en Annexe une section verticale de ce modèle le long d’un des diamètres de la base : on admet alors que la section plane obtenue a une forme de trapèze. On appelle A, B, C, D ses sommets, puis O et M les centres respectifs de la base du cône et du petit disque de la section horizontale. On appelle S le sommet du cône tronqué.
Dans tout le problème, on calculera les longueurs en cm, les volumes en cm3, au centième près.
1) Calculer la hauteur du cône non tronqué.
2) En déduire le volume de ce cône, puis celui du pastel dans ce modèle.
On rappelle la formule du volume V d’un cône de rayon R et de hauteur h : V = πR2h/3.
3) Dans ce modèle, a-t-on OC = OB ? Justifier la réponse.
4) Pour modéliser la pâte feuilletée qui entoure le pastel, on applique au cône tronqué, une homothétie de centre O de rapport 8/9. Cette homothétie forme alors un autre cône tronqué, plus petit, dont la coupe verticale donne un autre trapèze qu’on nommera A’B’C’D’.
Représenter directement sur la section verticale (à droite en Annexe) le trapèze A’B’C’D’.
5) L’intérieur du petit cône tronqué ainsi formé contient alors la crème (on admettra totalement), alors que la partie située entre le bord du cône tronqué d’origine et ce petit cône représente la pâte feuilletée. On appellera M’ l’image de M par l’homothétie décrite à la question 4).
a) Montrer que, dans ce modèle, l’épaisseur de la couche de pâte feuilletée n’est pas constante (on pourra pour cela, par exemple, calculer les distances BB’ et MM’).
b) Dans ce modèle, à quel endroit se situe l’épaisseur de couche de pâte feuilletée la plus importante ? Justifier la réponse.
6) Calculer, dans ce modèle, le volume de crème contenue dans le pastel.
Annexe