Niveau : Première (Spécialité Maths)
Chapitres : Produit scalaire
Inédit, publié le 28/09/2023

Note: sur la version en ligne du problème, les vecteurs et angles sont écrits en gras italique.
Ceux qui possèdent une tablette savent que c’est un objet fragile qu’il vaut mieux protéger. Les coques, qui couvrent aussi bien l’arrière de l’appareil que la vitre à l’avant, deviennent alors presque impératives. Elles peuvent, comme dans le cas que nous allons étudier dans ce problème, faire un peu plus que simplement protéger.
Sur la coque dont on peut voir l’image ci-dessus, la protection de la vitre prend la forme d’une page solide qui se divise en trois bandes verticales. Repliée en arrière, la protection forme un support similaire à un prisme à base triangulaire sur lequel la tablette peut reposer. Cela permet de libérer les mains et de faciliter la lecture.
Une vue de face et de côté de cette tablette protégée est proposée en Annexe avec quelques dimensions. Sur le côté, des points-clés de la tablette et de la protection repliée, nommés avec les lettres de A à E, ont été placés et reliés. L’objectif de ce problème est de trouver l’angle du support de lecture α (c’est à-dire l’angle BAD).
On pourra, dans ce problème, arrondir toutes les valeurs obtenues au dixième près.
1) En utilisant les longueurs des côtés, calculer le produit scalaire CD.CB.
2) A l’aide d’une autre expression de ce produit scalaire, déterminer, en degrés, l’angle BCD.
3) a) Calculer le produit scalaire CA.CB.
b) En déduire la longueur AB, en cm.
4) a) Dans le triangle ABD, donner l’expression de l’égalité du théorème d’Al-Kashi contenant l’angle α.
b) En déduire la valeur, en degrés, de l’angle de lecture α.
Pour aller plus loin : une très belle extension de ce problème (Grand Oral ?) serait de poser la question suivante : quelle est la valeur de a (largeur de DC ou BC) qui permet d’obtenir l’angle de lecture le plus grand ?
Annexe
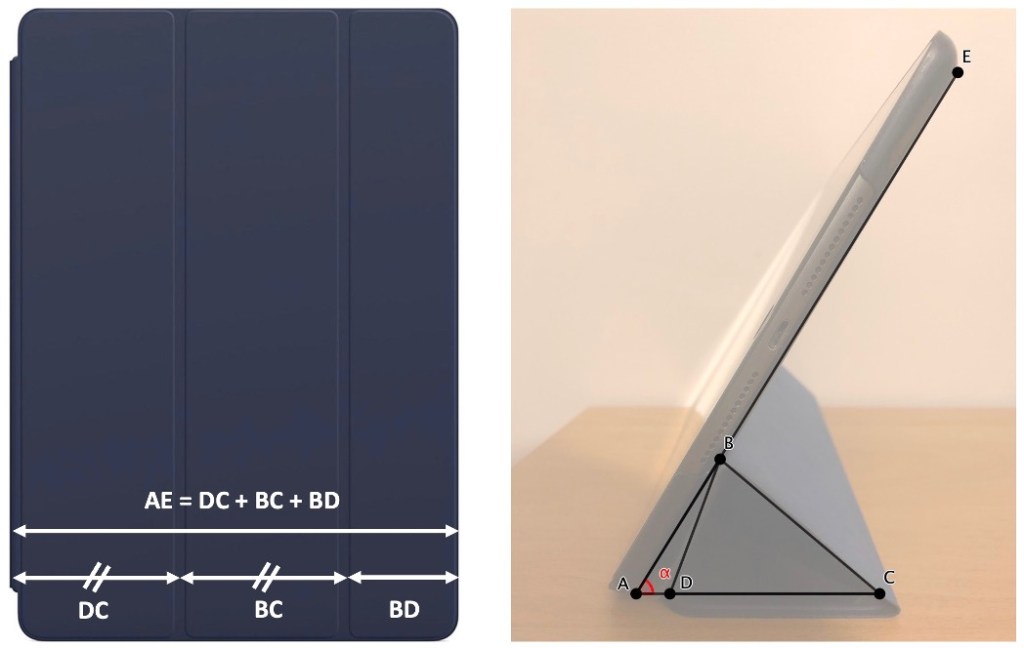
Dimensions :
AE (largeur de la protection) : 17,5 cm
a = DC = BC (largeur de chacune des deux premières bandes de la protection) : 6,5 cm
AD (espace séparant le triangle de la tablette) : 1 cm