Problème 408 – Espérance au Mikado

Niveau : Première (Spécialité Maths)
Chapitres : Probabilités, Variables aléatoires
Inédit, publié le 23/09/2023

            Jeu familial par excellence, le Mikado consiste à retirer un à un des bâtonnets de bois qui ont été empilés sur la table en vrac, comme sur la photo ci-dessus. La difficulté est de ne rien faire bouger d’autre que le bâtonnet que l’on retire. Ce jeu requiert du doigté et surtout de la patience !

            Les bâtonnets, traditionnellement au nombre de 41, donnent un nombre de points variable selon le motif qu’ils portent. Ces nombres de points, et le nombre de bâtonnets de chaque type, sont résumés dans le Tableau 1 ci-dessous.

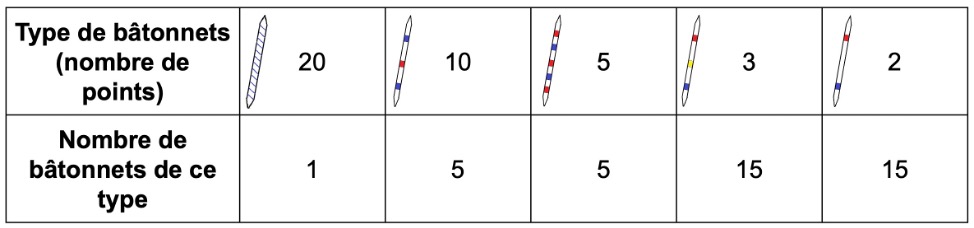
            On suppose que l’on prend au hasard, au milieu d’un paquet de bâtonnets tout juste empilés sur la table, un premier bâtonnet. On appelle X la variable aléatoire qui, à un bâtonnet retiré de l’empilement, associe le nombre de points obtenus.

Dans tout le problème, on arrondira les valeurs obtenues au centième près.

1) Établir la loi de probabilité de X.

2) Calculer l’espérance et l’écart-type de X.

3) a) Quelle est la probabilité que, en retirant un premier bâtonnet, on fasse diminuer la moyenne du nombre de points donnés par les bâtonnets restants sur la table ?

b) Quel est le nombre minimal de bâtonnets que l’on doit retirer pour que cette moyenne passe en dessous de 3 points ?

4) On souhaite modifier les règles du jeu de telle manière à ce que l’espérance de X, au début du jeu, soit égale ou supérieure à 5 points. On propose deux manières de le faire, de manière séparée:

a) Soit on augmente la valeur des points des bâtonnets valant 3 points. Quelle devrait être au minimum la nouvelle valeur de ces bâtonnets, sachant que cette valeur reste un nombre entier de points ?

b) Soit on ajoute au paquet des bâtonnets valant 10 points. Combien faudrait-il en rajouter, au minimum ?