Problème 391 – Wazabi

Niveau : Troisième
Chapitres : Probabilités
Inédit, publié le 05/06/2023

            A la fois un jeu de dés et un jeu de cartes, Wazabi, créé en 2008, est très simple à comprendre. Chaque joueur.se possède 4 dés à 6 faces au départ et doit s’en débarrasser le plus vite possible directement à l’aide des dés ou l’aide de cartes. Pour cela, à son tour, il ou elle lance les dés, suit leurs instructions, puis joue une seule carte à condition que ce lancer de dés le lui permette. Dans ce problème, nous allons étudier des situations de fin de jeu pour voir la probabilité de gagner en fonction des cartes possédées ou non.

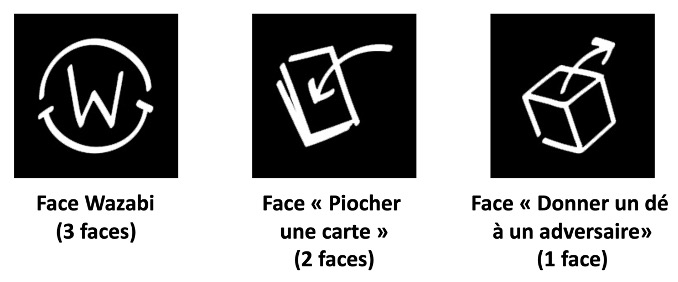
            Décrivons d’abord les dés et les cartes. Tous les dés sont équilibrés et identiques et un dé possède 3 types de faces : face « Wazabi » (visible sur 3 faces du dé), face « Piocher une carte » (sur 2 faces), et une face « Donner un dé à un adversaire » (sur une seule face) (voir Annexe 1). Les cartes, elles, donnent chacune une instruction. Le joueur qui voudrait utiliser une carte à son tour après son lancer de dés ne peut le faire que si le nombre de faces « Wazabi » qui apparaissent au lancer est au moins égal au nombre de « Wazabi » visibles sur la carte, en haut, à gauche (voir exemple en Annexe 2).

            On se rend compte alors qu’il est de plus en plus difficile de gagner au fur et à mesure que l’on a moins de dés puisque de nombreuses cartes ne sont utilisables que si on a deux faces « Wazabi » ou plus (ce qui est impossible avec un seul dé lancé).

Partie A

Jonathan joue au Wazabi et n’a plus qu’un seul dé.

1) Supposons d’abord que Jonathan n’a aucune carte en main. Il lance le dé.

a) Quelle est la probabilité que la face qui apparaît soit une face « Donner un dé à un adversaire » ? 

b) Aucune carte ne permet à Jonathan de se débarrasser du dé s’il ne fait pas apparaître au moins une face « Wazabi » dans le lancer de dés^(*).

Jonathan pourrait-il quand même gagner immédiatement avec un autre type de face que « Donner un dé à un adversaire »?

2) On suppose maintenant que Jonathan n’a plus qu’un seul dé à jeter, mais aussi la carte en main visible en Annexe 2. On admet que cette carte est la seule qui permet, pour un joueur qui n’aurait qu’un seul dé, de s’en débarrasser (hors tirage du dé avec la face « Donner un dé à un adversaire »).

Quelle est alors la probabilité pour Jonathan de gagner immédiatement sur ce coup de dé ?

Partie B

Dans cette partie, on s’intéresse maintenant au cas de Ludovine, qui a encore deux dés à jeter.

3)  Supposons que Ludovine ne possède aucune carte.

a) Remplir le Tableau 1 ci-dessous qui donne le nombre MAXIMAL de dés que Ludovine pourrait donner ou supprimer en fonction des faces observées lors du lancer des deux dés.

Tableau 1

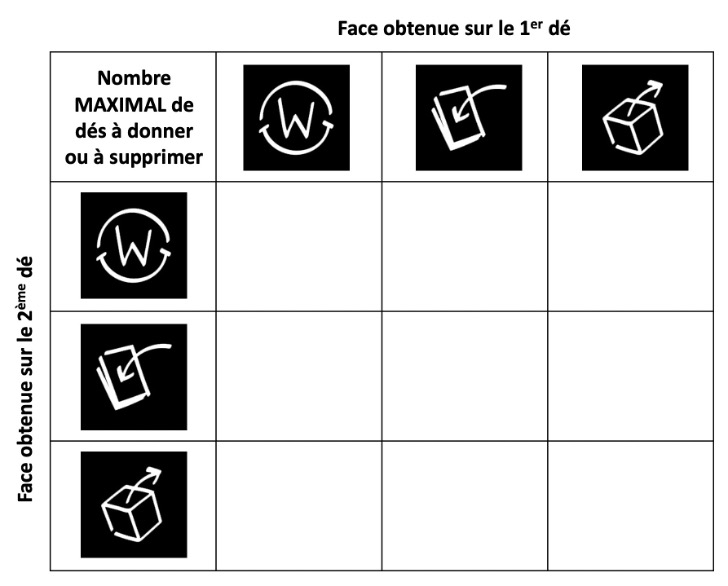
b) Ludovine estime, d’après le tableau précédent, que sa chance de gagner immédiatement en lançant les deux dés est égale à 1/9. Expliquer d’où vient le raisonnement de Ludovine, et montrer pourquoi ce raisonnement est incorrect.

c) Calculer alors la véritable probabilité pour Ludovine de gagner immédiatement en lançant les deux dés (on pourra, si besoin est, faire un autre tableau).

4) Étudions maintenant le cas où elle possède une carte comme celle visible en Annexe 2.

Calculer dans cette situation la nouvelle probabilité pour Ludovine de gagner immédiatement sur ce coup de dés. 

Annexe 1
Faces possibles des dés

Annexe 2

(*) Aux connaisseurs du jeu : dans tout le problème, pour simplifier la modélisation, on ignorera donc ici la carte « Rejouer et changer de sens », qui compliquerait sensiblement le calcul.