Niveaux : Terminale (Option Maths Expertes)
Chapitres : Graphes
Inédit, publié le 17/02/2026 (Bonne année du Cheval!)

La ville de Saïgon, aujourd’hui nommée Hô-Chi-Minh-Ville (souvent abrégée HCMC pour Ho Chi Minh City), est la ville la plus importante du Vietnam, bien qu’elle n’en soit pas la capitale. Avec une population de près de 10 millions d’habitants et une surface très étendue, son découpage administratif a souvent fait l’objet de modifications. La notion de « district » (en vietnamien : « Quận») a été utilisée pendant des décennies et reste encore très courante dans les usages, bien qu’elle ait été révolue en 2025 par une nouvelle structure. Dans ce problème, nous vous proposons de voyager dans cette ville et ses districts aujourd’hui disparus… car sait-on jamais si, un jour, vous aurez la chance de découvrir cette perle si dynamique de l’Asie du Sud-Est ?
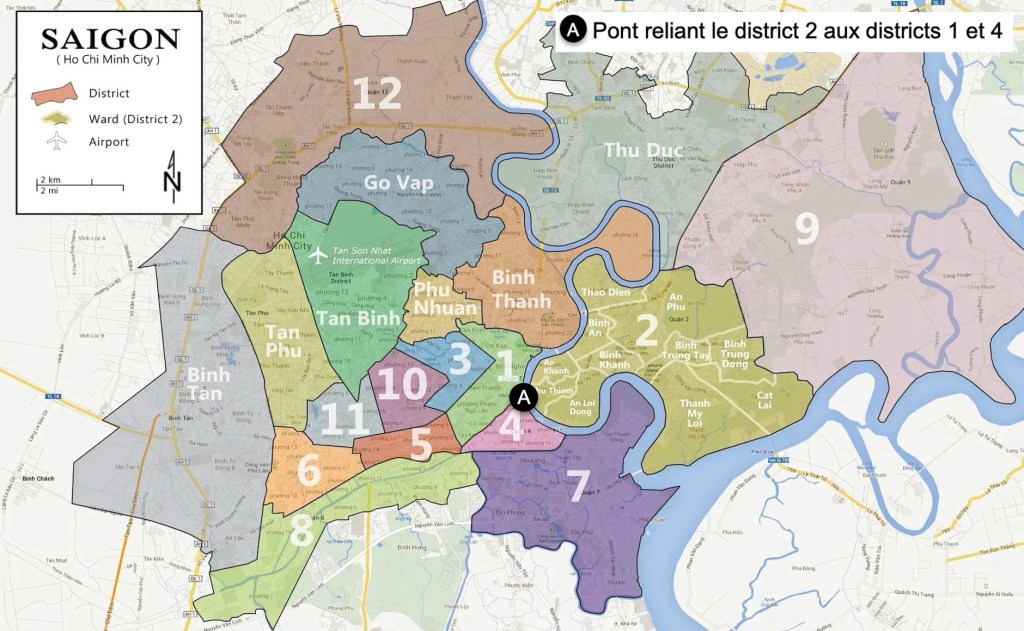
Jusqu’en 2020, la ville de HCMC se divisait en 24 districts, dont 19 urbains : parmi ces derniers, 12 étaient numérotés (de 1 à 12) et 7 portaient des noms, comme on peut le voir sur une ancienne carte visible en Annexe 1(1).
1) Dans un premier temps, on s’intéresse aux quartiers principaux du centre-ville, qui se regroupent principalement autour du district 1 – là où se trouve le cœur de ville (et notamment le fameux marché Bến Thành !). On ne s’intéresse qu’aux districts 1, 2, 3, 4, Phú Nhuận (PN) et Bình Thắng (BT). On considère que deux districts sont directement reliés s’il existe une frontière ou un pont entre les deux.
a) Construire un graphe non orienté et non pondéré avec ces six districts, chacun représentant un sommet.
Remarque : le pont marqué par la lettre A permet de relier le district 2 à la fois au district 1 et au district 4 : pour simplifier, il pourra être séparé en deux arêtes distinctes.
b) Déterminer dans ce graphe une chaîne de longueur 5 reliant le district Phú Nhuận au district 4.
2) a) Établir la matrice d’adjacence associée au graphe établi à la question 1).
b) Dans ce graphe, combien de chaînes de longueur 5 relient le district 2 au district 3 ?
3) En étudiant les degrés de tous les sommets du graphe précédent, montrer qu’il n’existe pas de chaîne eulérienne dans ce graphe, c’est-à-dire de chaîne passant par toutes les arêtes exactement une seule fois.
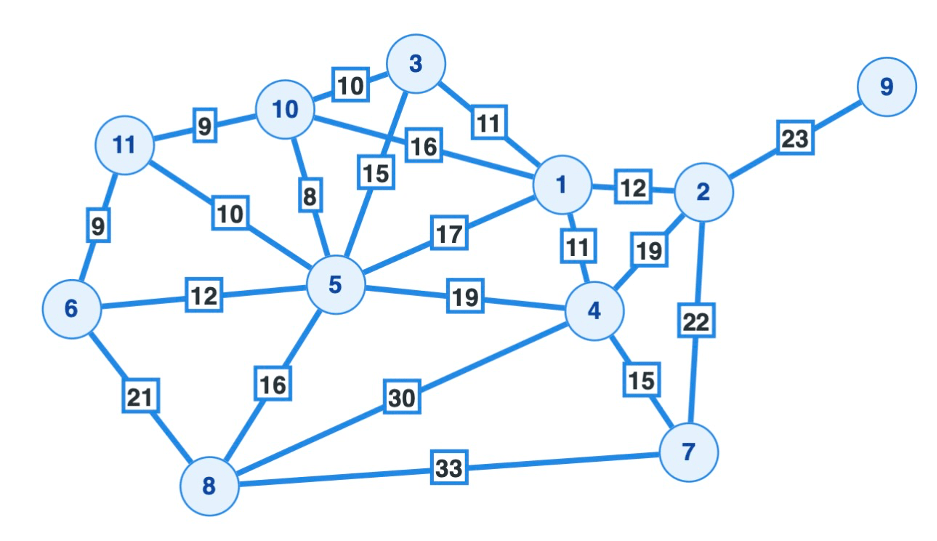
4) Maintenant, on établit un graphe pondéré avec pour sommets les districts numérotés de 1 à 11, en indiquant le temps de parcours en minutes nécessaire entre deux districts adjacents, ou du moins entre leurs lieux principaux respectifs, selon Google Maps. Ce graphe est visible en Annexe 2.
Déterminer de deux manières possibles la somme des degrés de ce graphe.
5) A l’aide de l’algorithme de Dijkstra, établir quel est le chemin le plus court(2) :
• qui relie le district 6 au district 9.
• qui relie le district 7 au district 10.
Annexe 1(1)
Annexe 2(3)
(1) Source : https://codiemaps.wordpress.com/2013/07/27/district-map-of-ho-chi-minh-city/
(2) Il est vrai qu’en réalité, un parcours le plus court ne nécessiterait pas un passage par les lieux principaux des districts, mais nous pourrons ignorer ce point ici…
(3) Graphe réalisé avec Graph Online