Niveaux : Première (Spécialité Maths)
Chapitres : Polynômes du second degré
Inédit, publié le 31/12/2025
Remarques de l’auteur : tout comme pour les deux années précédentes, ce problème de fin d’année rend hommage au peuple ukrainien pour son immense résilience.

« Slava Oukraïni ! » (en ukrainien : « Слава Україні ! ») ou « Gloire à l’Ukraine ! ». Au bout de quatre années de résistance acharnée contre l’invasion russe, l’Ukraine ne plie pas, et il faut espérer qu’elle puisse tenir jusqu’à obtenir une paix juste. Une inconnue de taille demeurera cependant : qu’en sera-t-il de la population ukrainienne quand les armes se tairont ? Avant même de s’effondrer littéralement avec le conflit, la population de l’Ukraine était déjà en baisse depuis 1993. Pourra-t-elle un jour croître à nouveau pour faire briller le pays ? Dans ce problème, nous étudions les chiffres de population de ce peuple courageux, qui doit refuser autant les sombres prédictions que les diktats étrangers.
On étudie pour ce problème les évolutions de la population de l’Ukraine depuis 1960, date à laquelle les chiffres commencent à être disponibles auprès de la Banque Mondiale(1). A partir des données, il est possible d’observer que la population de l’Ukraine a suivi deux trajectoires majeures : l’une de croissance jusqu’en 1993, l’autre de décroissance de 1993 à 2022, année du début de la guerre. Considérons la fonction qui au temps t en années écoulées après 1960 (fin d’année) associe la population de l’Ukraine en millions.
Sur l’intervalle [0 ; 33], on admet que f est égale à une fonction f1 telle que :
f1(t) = -0,00554t2 + 0,461t + 43,1.
Sur l’intervalle [33 ; 61], on admet(2) que f est égale à une fonction f2, qui est aussi un polynôme du second degré, d’expression :
f2(t) = at2 + bt + c avec a,b,c ∈ ℝ
La représentation graphique de f sur l’intervalle [0 ; 61] est visible en Annexe.
Sur l’ensemble du problème, on laissera les valeurs demandées avec trois chiffres significatifs.
1) Conjecturer graphiquement, puis justifier algébriquement en quelle année la population de l’Ukraine a atteint 50 millions d’habitants pour la première fois.
2) a) Dans l’expression de f2(t), justifier à l’aide d’un argument graphique le signe de a.
b) Après 1993, la population de l’Ukraine est repassée en dessous de 50 millions d’habitants en 1999. On admet par ailleurs que dans l’expression de f2(t), on a c=70,4.
Déterminer les valeurs de a et b et en déduire une expression complète de f2(t).
c) En déduire la population de l’Ukraine, selon ce modèle, fin 2021.
3) Si la guerre n’avait pas débuté et que la population de l’Ukraine avait continué à diminuer en suivant la tendance donnée par l’expression de f2, en quelle année la population aurait-elle atteint un minimum ? Quelle aurait été la population à ce moment-là ?
4) Malheureusement, fin 2024, la population de l’Ukraine était estimée à seulement 37,8 millions d’habitants – bien en-dessous des niveaux observés entre 1960 et 2021. Des projections(3) estiment que l’Ukraine pourrait tomber à 15 millions d’habitants en 2100 mais… on est en droit de refuser ces projections et d’en créer d’autres plus optimistes !
a) Déterminer l’expression d’une fonction affine f3 définie sur l’intervalle [64 ; 100] avec f3(64) = 37,8 qui verrait l’Ukraine réatteindre 50 millions d’habitants en 2060.
b) De même, déterminer l’expression d’une fonction polynôme du second degré f4 définie sur l’intervalle [64 ; 100] avec f4(64) = 37,8 qui verrait l’Ukraine réatteindre 50 millions d’habitants en 2060 en ayant atteint 40 millions en 2035 (si nécessaire, on pourra utiliser la calculatrice pour résoudre le système posé).
c) Tracer sur le graphique en Annexe les courbes représentatives de f3 et f4 sur l’intervalle [64 ; 100].
Annexe
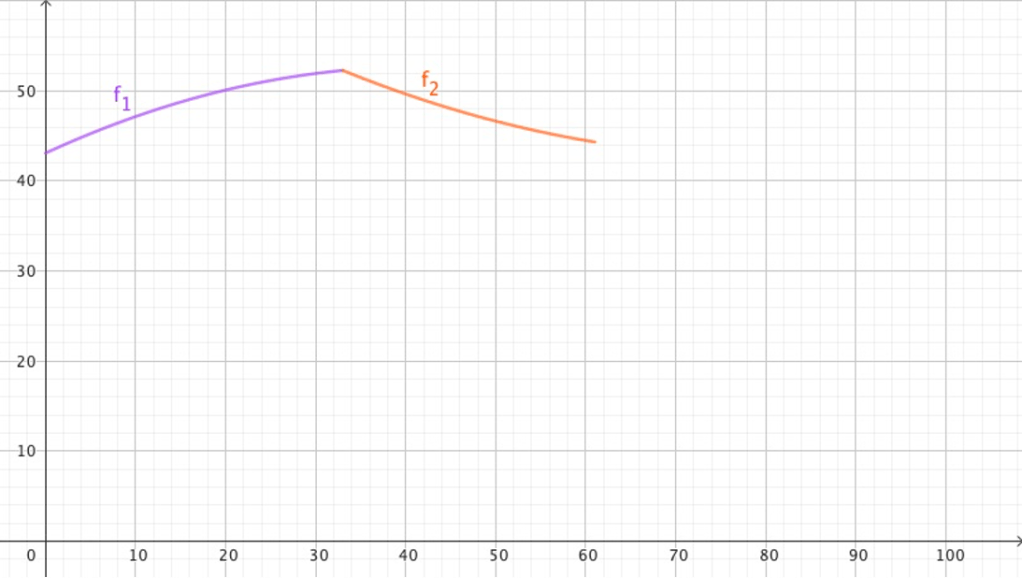
(1) Source : https://donnees.banquemondiale.org/indicateur/SP.POP.TOTL?locations=UA
(2) Une fonction polynôme du troisième degré ou même du cinquième degré serait plus proche des valeurs réelles mais nous admettons l’approximation ici.
(3) Source :https://www.intellinews.com/ukraine-s-population-will-crash-to-a-mere-15mn-people-by-2100-un-333727/