Problème 561 – La pétition contre la loi Duplomb

Niveaux : Terminale (Option Maths complémentaires)
Chapitres : Convexité
Inédit, publié le 30/10/2025

Durant l’été 2025, la pétition contre la loi Duplomb a établi un record en devenant la pétition déposée à l’Assemblée Nationale la plus soutenue de l’Histoire, avec plus de 2 millions de signatures. Cette loi avait pour objectif initial de lever des contraintes au métier d’agriculteur : cependant, elle fit face à une très forte opposition dans l’opinion publique car elle souhaitait permettre la réintroduction d’un insecticide, l’acétamipride, connu pour sa dangerosité pour les abeilles. Cette disposition de la loi fut l’objet d’intenses débats, avant qu’elle ne soit censurée par le Conseil Constitutionnel – même si une grande partie du reste de la loi fut promulguée.

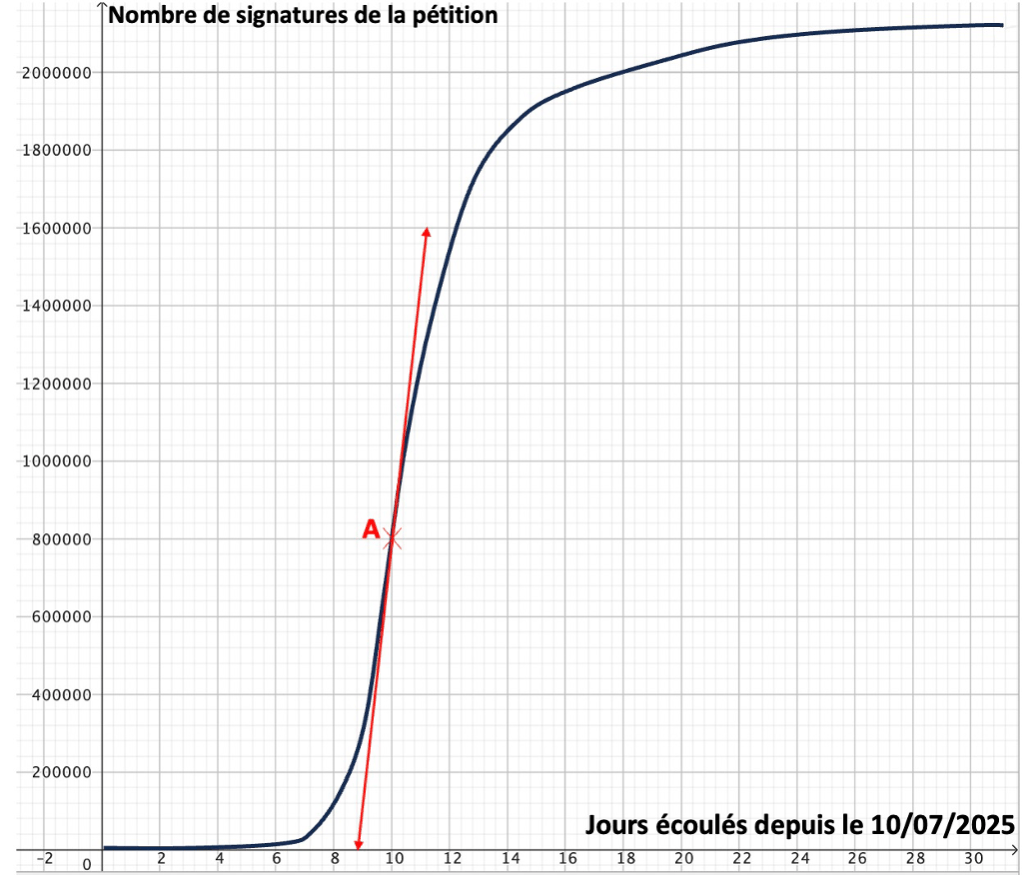
Le 10 juillet 2025, cette pétition fut lancée officiellement par une étudiante, Éléonore Pattery⁽¹⁾. Dans ce problème, nous allons regarder, grâce au suivi effectué par le journal Le Monde⁽²⁾ le nombre de signataires au jour le jour dans le premier mois de la pétition. On considère une fonction f qui au nombre t de jours écoulés après le 10 juillet (qui correspond donc à t=0) associe le nombre de signataires de la pétition. La courbe représentative de la fonction est visible en Annexe : elle a été dessinée sur l’intervalle [0 ; 31], correspondant au premier mois de la pétition. On admet que la courbe n’admet qu’un seul point d’inflexion (nommé A) sur cet intervalle, à t₀ = 10.

1) Déterminer graphiquement le jour où le nombre de signataires de la pétition a dépassé 2 millions.

2) a) Au point d’inflexion de la courbe, déterminer graphiquement la valeur de f'(t₀). (arrondir la valeur trouvée au millier près).

b) Expliquer ce que signifie ce point d’inflexion dans le contexte de la pétition.

3) a) Déterminer graphiquement les intervalles sur lesquels f est respectivement convexe ou concave.

b) En déduire, sur l’intervalle [0 ; 31], le tableau de signes de f’ ‘ (la dérivée seconde de f), puis le tableau de variations de f’ (on ne cherchera pas les valeurs de f’ aux bornes de l’intervalle).

4) a) Quel est le signe de f’ sur l’intervalle [0 ; 31] ?

b) Montrer, dans le contexte du problème, qu’il n’est pas imaginable que f’ change de signe pour t > 31.

5) a) Lire graphiquement la valeur approximative vers laquelle semble se diriger f(t) quand t devient très grand.

b) Dans quelle situation liée à la pétition pourrait-on imaginer qu’il y ait, en prolongeant la courbe pour t > 31, un autre point d’inflexion très marqué, puis un changement de convexité sur plusieurs jours ou semaines ?

Annexe