Niveaux : Première (Spécialité Maths)
Chapitres : Trigonométrie
Inédit, publié le 06/08/2025
A la mode depuis quelques années, le bracelet à « charms », ces ornements ou pendentifs décoratifs, font le bonheur des ados qui sont ravi(e)s de pouvoir porter au bras les signes distinctifs de leur personnalité. Certains et certaines n’hésitent pas à porter les personnages qui ont bercé leur enfance, comme par exemple Lou qui reste fan depuis toujours de Stitch, ce petit personnage extra-terrestre qui a trouvé l’amitié avec Lilo, et qui dans de plus récents épisodes a trouvé son amoureuse, nommée Angel (souvent connue sous le nom de « Stitch Rose »). Stitch et Angel se retrouvent maintenant au bras de Lou.
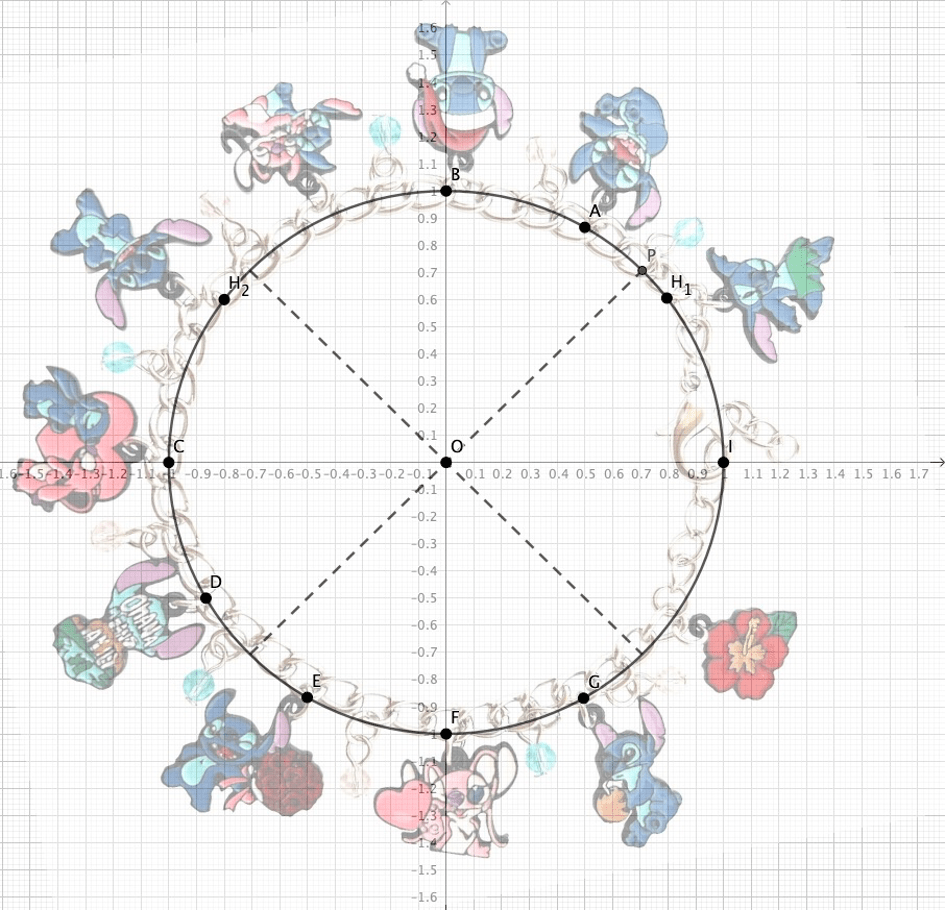
Le bracelet à charms de Lou est celui représenté en Annexe. Lou a très soigneusement positionné ses différents charms tout autour du bracelet, que nous allons, pour ce problème, assimiler à un cercle trigonométrique de centre O. Ce cercle est tel que le point de fermeture du bracelet se situe tout proche du point image I associé au réel 0.
1) Certains charms ont été attachés au bracelet précisément aux points images A, B, C, D, E, F et G, comme on peut le voir sur le schéma en Annexe.
Donner pour chacun de ces charms le nombre dans l’intervalle ]-π ; π] associé au point image où il est attaché.
2) a) Convertir la valeur trouvée pour le point E en degrés.
b) A la mesure de quel angle cette valeur correspond-t-elle ?
3) Décrire les charms dont les points d’attache au bracelet sont les plus proches des points image associés aux valeurs -16π/3 et 47π/6.
4) Une perle est attachée au point P du cercle trigonométrique (en haut à droite), précisément sur une des deux diagonales principales (en pointillés). On appelle α la mesure principale respective associée à ce point. Que valent cos α et sin α?
5) Deux charms sont positionnés à proximité de deux points H1 et H2 symétriques par rapport à l’axe des ordonnées, comme on peut le voir sur le schéma en Annexe. On appelle β et ɣ les mesures principales respectives associées à chacun de ces deux points. On voit que sin β = sin ɣ = 0,6.
a) Justifier par le calcul la valeur de cos β et cos ɣ.
b) Donner la valeur de β et de ɣ en radians (arrondir au centième près).
6) Lou veut ajouter un charm près du point de fermeture (là où il reste de la place !). Ce charm, associé à un point d’image δ doit donc être tel que cos δ > 0,9 et sin δ < 0.
Déterminer sur l’intervalle ]-π ; π], puis sur l’intervalle [0; 2π[, la condition que doit respecter δ pour que le charm soit placé correctement sur le bracelet.
Annexe