Niveaux : Troisième
Chapitres : Théorème de Pythagore, Trigonométrie, Théorème de Thalès
Inédit, publié le 25/07/2025

Remarque: dans la version en ligne, les angles sont écrits en gras italique.
Émission créée en 1962, Intervilles fait partie de ces jeux télévisés mythiques qui reviennent parfois pendant l’été, comme en 2025. Ce jeu fait affronter des villes autour de jeux spéciaux, dont le fameux « mur des champions » qui, depuis plus de 20 ans, est l’épreuve finale qui couronne la ville vainqueur : il s’agit pour les concurrents de gravir un mur incliné composé d’échelons, uniquement à la force de leur bras en s’appuyant sur une barre qui peut s’accrocher à chaque échelon. Dans ce problème, nous nous proposons d’étudier les caractéristiques de ce mur qui est désormais presque aussi connu que l’émission elle-même.
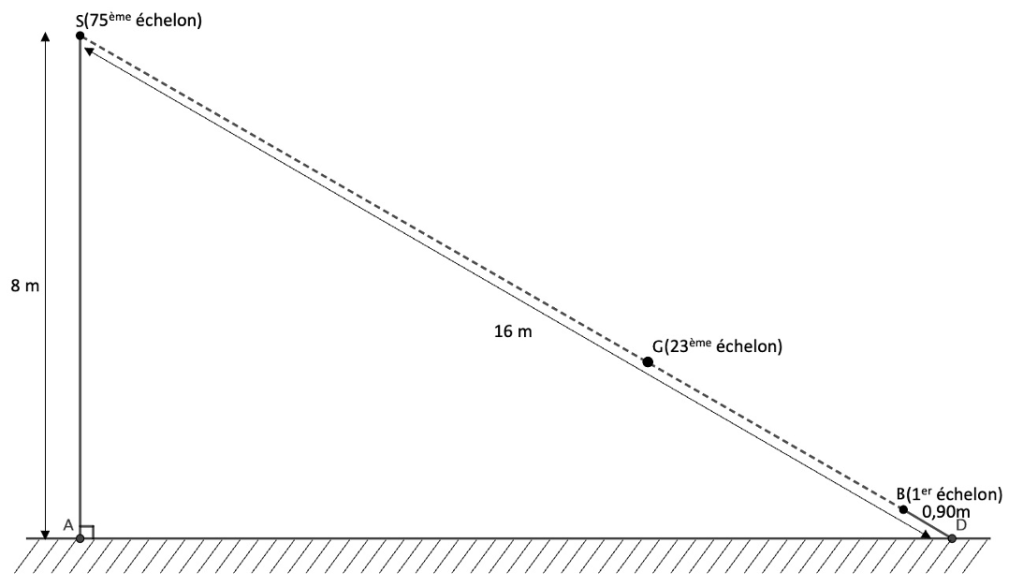
On a représenté ce mur sur le dessin en Annexe : incliné entre les points D (au départ) et S (au sommet), ce mur forme avec le point A au sol, à la verticale du point S, un triangle ADS rectangle en A. Le point S se situe à 8 m de hauteur, alors que la longueur DS du mur est de 16 m.
Dans tout le problème, on arrondira si nécessaire les valeurs obtenues au centième près. Toutes les longueurs seront calculées en mètres.
1) Calculer la longueur AD.
2) Quel est le degré d’inclinaison du mur, représenté par la mesure de l’angle ADS ?
3) Le 1er échelon du plan, au point B, est situé sur le plan incliné à 0,90 m du point de départ D, alors que le 75ème échelon se situe au point S. On suppose que la distance entre deux échelons successifs est toujours la même.
a) Calculer la distance entre deux échelons successifs.
b) Déterminer à quelle hauteur verticale se situe le point B.
4) Lors de la finale en 2025, remportée par Gap, le premier candidat à s’élancer pour cette ville était parti du 23ème échelon, car la ville avait gagné 23 points tout au long de l’émission. Sur le schéma en Annexe, on appelle G le point du segment [DS] d’où est parti ce candidat.
a) A quelle hauteur verticale se situait ce candidat quand il a commencé à gravir le mur ?
b) A quelle distance se situait-il alors du point A ?
Indication : on pourra s’appuyer sur la projection orthogonale de G au sol.
c) Calculer la mesure de l’angle SGA.
Annexe