Niveaux : Première (Tronc commun/Technologique)
Chapitres : Dérivation
Inédit, publié le 16/02/2025

Chaque année, quand commence une année de lycée pour les élèves de 2nde ou de 1ère, de nombreux élèves vivent sans le savoir l’effet de Dunning-Kruger. Quand ces élèves commencent l’étude d’un chapitre, ou plus généralement leur année scolaire, ils ou elles estiment, en s’appuyant sur leur scolarité passée trop facile, que peu de connaissances suffisent pour tout comprendre et ainsi réussir : c’est un phénomène appelé de surconfiance. Mais à l’inverse, quand ces élèves creusent un peu plus, ils ou elles ont soudain l’impression de ne plus rien comprendre : ces élèves ne sont alors qu’au début de la fameuse courbe de l’effet de Dunning-Kruger, qui va servir de base pour ce problème.
Prenons l’exemple de Jean, un élève qui a traversé cet effet de Dunning-Kruger sur toute son année de Seconde. Avec une mention très bien au DNB, il pensait pouvoir tout comprendre très vite rien qu’en écoutant en cours. Puis, voyant la difficulté des leçons croître, il s’est mis au travail mais a connu une phase de crise où il ne pensait plus rien comprendre à chaque leçon. Mais avec persévérance, il s’est ressaisi pour regagner de la confiance et atteindre en fin d’année un niveau réel de compétence bien supérieur à ce qu’il croyait avoir au départ.
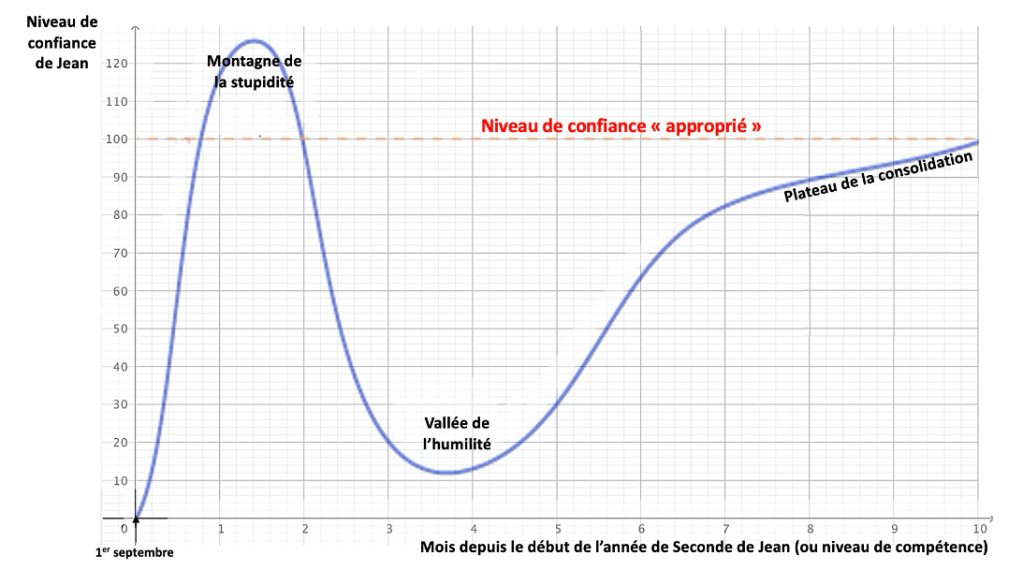
Pour modéliser l’évolution de la confiance en Jean en fonction du temps (et donc de sa compétence réelle), on utilise la courbe typique de l’effet de Dunning-Kruger dessinée dans le graphique en Annexe. On considère qu’elle est représentative d’une fonction f qui, au temps t en mois depuis le début de l’année de Seconde de Jean en septembre, associe une valeur de sa confiance tout au long de cette année scolaire. 100 est la valeur arbitraire de référence, sans unité, qui représente une confiance « appropriée » : ni trop basse, ni trop haute.
1) Expliquer pourquoi le premier maximum de la courbe est appelé « la montagne de la stupidité » et pourquoi le minimum local qui suit est appelé « la vallée de l’humilité ».
2) Comment peut-on voir sur la courbe qu’à partir de Novembre, Jean a plutôt eu tendance à se sous-estimer ?
3) A partir de la courbe dessinée en Annexe, dresser le tableau de variations de f puis en déduire le tableau de signes de f‘.
4) a) On donne f‘(6)=30. Quelle est l’équation de la tangente à la courbe quand t = 6 ?
b) Écrire ce que signifie f'(6) dans le contexte du problème, et donner son unité.
Indication : on pourra utiliser le mot « vitesse ».
5) a) Déterminer graphiquement à quel moment t0 la valeur de f’ semble maximale, et trouver la valeur de f'(t0).
b) Déterminer graphiquement à quel moment t1 la valeur de f’ semble minimale, et trouver la valeur de f'(t1).
c) Quand ils sont arrivés, pourquoi chacun de ces deux moments, l’un comme l’autre, pouvaient être considérés comme dangereux dans l’évolution de la confiance de Jean en Seconde ?
Annexe