Niveaux : Terminale (Spécialité Maths)
Chapitres : Fonctions (Continuité, Limites)
Inédit, publié le 21/01/2025

D’hiver en hiver, la bottine continue d’être est la chaussure indémodable qui permet de combiner protection contre le froid et élégance. Elle convient à tous les publics, en offrant un contour classique et facile à reconnaître: parfaitement courbé du talon au pied, le profil de la bottine peut se modéliser très simplement à l’aide de quelques courbes standard. Nous nous proposons de les étudier dans ce problème.
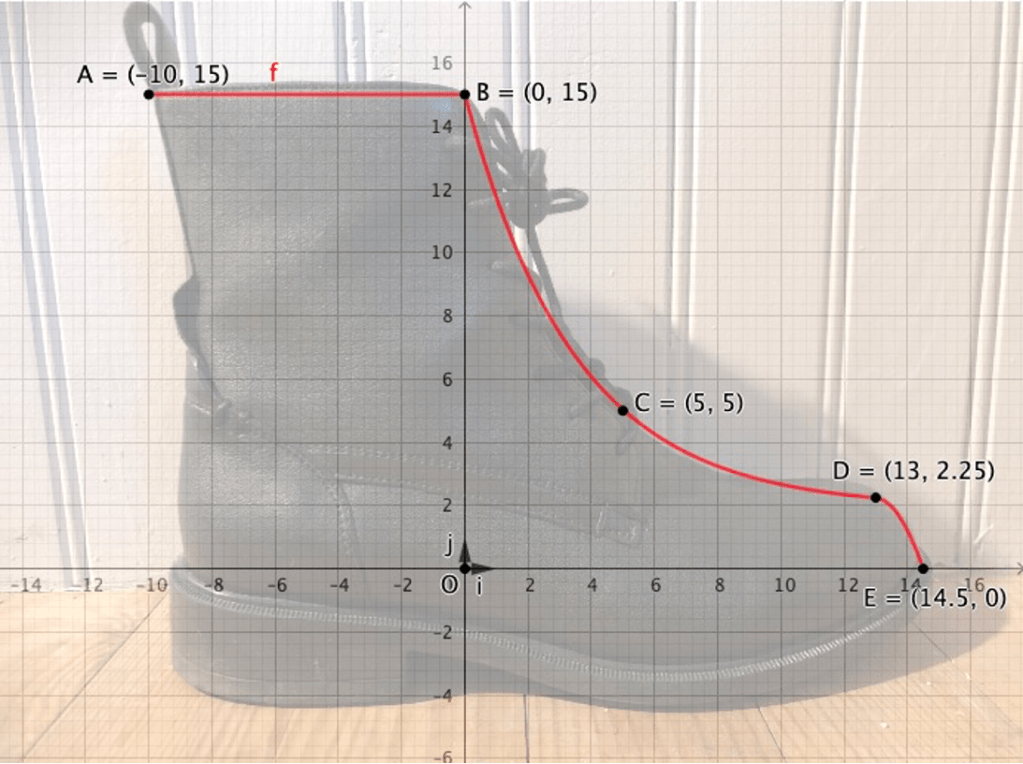
Le modèle que nous allons étudier est celui proposé sur le schéma en Annexe. Dans un repère orthonormé (O, i, j) avec une unité en cm, on a placé la photo de profil d’une bottine. On va étudier une courbe qui épouse le dessus de la chaussure, qui part d’un point A(-10 ;15) à l’arrière pour aller jusqu’au point E (14,5 ; 0) au bout de la chaussure. La courbe en question, représentative d’une fonction f et tracée en rouge sur le schéma, est composée de 3 parties :
Partie 1 (arrière, pour l’entrée du pied): horizontale entre les points A et B(0 ; 15).
Partie 2 (centrale) : en nette descente entre les points B et D(13 ; 2,25).
Partie 3 (avant, en bout de chaussure) : légèrement courbée entre les points D et E.
L’objectif de ce problème est de déterminer les expressions de la fonction f sur chacune de ces trois parties.
Dans tout le problème, on arrondira, si nécessaire, les valeurs obtenues à 10-3 près.
1) Rappeler l’expression de la fonction f sur la partie arrière entre les points A et B.
2) On cherche à modéliser la partie centrale sur l’intervalle [0 ;13] par une fonction de la forme exponentielle. On essaie dans un premier temps d’écrire cette partie de la fonction f sous la forme f(x) = aebx sachant que cette courbe doit passer par les points B et D.
a) Déterminer les valeurs de a puis de b dans cette approche.
b) On voit que le profil de la chaussure passe proche du point C(5 ; 5). Montrer que cela n’est pas le cas avec la fonction proposée en 2.a).
3) On propose alors d’ajuster le modèle en cherchant pour cette partie une fonction de la forme : f(x) = a’eb’x + c’.
Pour épouser au mieux le contour de la chaussure, on suppose que la courbe représentative de f, qui doit toujours passer par les points B et D, admet à droite du point B une tangente de coefficient directeur -3,75.
a) A l’aide d’un argument de limite en +∞, justifier que le profil de la courbe implique que b'<0.
b) La courbe passant par les points B et D, écrire un système de 3 équations avec les inconnues a’, b’ et c’.
c) Montrer que la résolution de ce système amène à la résolution de l’équation :
15e13b’– 51b’ – 15 = 0
4) On pose la fonction g définie sur l’intervalle ]-∞;0[ par : g(x)= 15e13x – 51x – 15.
a) Établir le tableau de variations de la fonction g.
b) En déduire que la fonction g admet une unique racine x0. En donner une valeur approchée à l’aide de la calculatrice.
c) En déduire les valeurs de a’ et c’.
d) Vérifier que la fonction proposée passe bien à proximité du point C.
5) La partie avant est en continuité de la partie centrale. Comme on ne veut pas avoir de « cassure » dans le contour de la courbe, on doit non seulement respecter la continuité de f au point D, mais aussi celle de f’. La courbe à l’avant passe par le point E.
L’arrondi de la forme à l’avant nous amène à chercher une modélisation du profil sur l’intervalle
[13 ; 14,5] avec une fonction polynomiale de degré 2, de la forme f(x) = a »x2 + b »x + c ».
Poser et résoudre le système d’équations qui permet de déterminer les valeurs de a », b » et c ».
Annexe