Niveaux : 2 versions : Sixième/Cycle 3 et Troisième
Chapitres : Calculs numériques, Angles, Longueurs (6ème)
Proportionnalité (Distance/Vitesse/Temps), Théorème de Pythagore, Trigonométrie (3ème)
Inédit, publié le 14/09/2024

Note: sur la version en ligne du problème, les angles sont écrits en gras italique.
Basé sur une émission d’origine japonaise, Sasuke, Ninja Warrior est arrivé en France à l’été 2016 et revient chaque année depuis. Dans ce jeu, des candidats s’attaquent à différents parcours d’obstacles sur lesquels ils n’ont généralement pas droit à l’erreur. Les très rares survivants qui passent toutes les épreuves ont le droit d’attaquer l’épreuve finale, nommée « La Tour des héros » . Pour y réussir et décrocher le pactole, un candidat doit réussir à grimper une corde de 23 mètres de hauteur en moins de 30 secondes. Autant dire qu’il vaut mieux être extrêmement athlétique !
Les deux problèmes sont strictement indépendants.
Problème Niveau 6ème / Cycle 3
En 2024, l’émission s’est déroulée dans le cadre du « Choc des Nations », où des concurrents de différents pays s’affrontaient. Ils étaient six en finale. Charles Poujade, le Français, a été le plus rapide. Les temps de tous les concurrents, dans leur ordre de passage, ont été indiqués dans le Tableau 1 ci-dessous.

1) a) Calculer l’écart de temps entre Charles Poujade et le concurrent le plus lent.
b) De combien de temps Charles Poujade a-t-il été meilleur que la limite traditionnelle de 30 secondes ?
2) « La somme des trois temps effectués par les concurrents français est inférieure à la somme des deux temps effectués par les concurrents venus des Etats-Unis » : cette affirmation est-elle correcte ? Justifier la réponse.
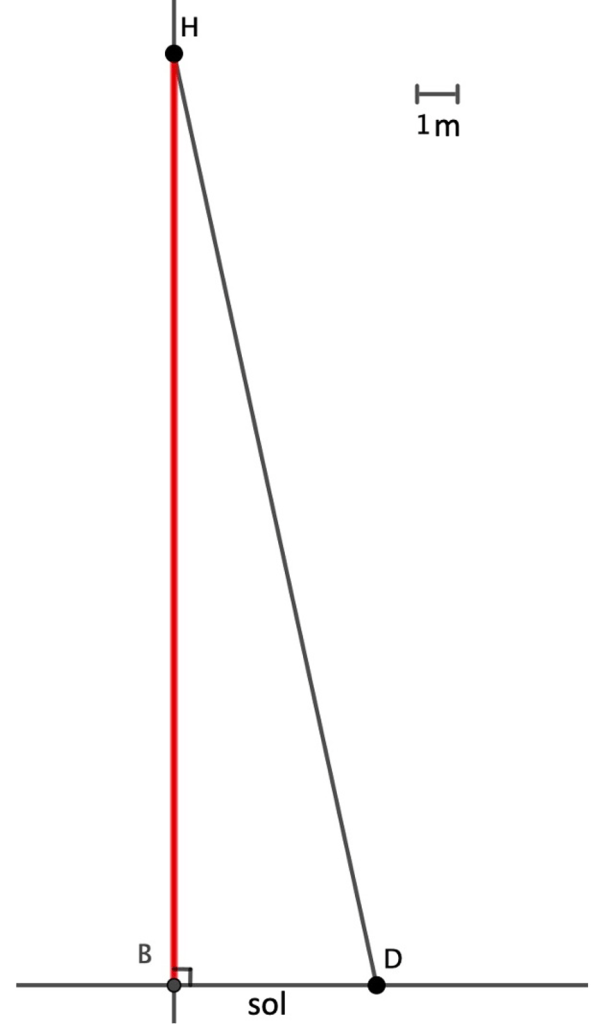
3) On a représenté, en Annexe, la corde de la Tour des héros par un segment vertical [BH] de longueur 23 m, B étant le point au sol et H le sommet. À quelques mètres de la corde, au sol, Denis Brogniart, le fameux présentateur de l’émission, regardait Charles grimper entre le B et le point H. Denis se trouvait au point D.
a) Mesurer à l’aide d’un rapporteur l’angle BDH et donner la valeur obtenue, arrondie au degré près.
b) Donner la nature de cet angle.
4) On appelle Q le lieu où était Charles Poujade au quart de la hauteur de la corde.
a) A quelle hauteur se trouvait Charles Poujade au point Q ?
b) Placer le point Q sur la figure en Annexe.
c) Mesurer à l’aide d’un rapporteur l’angle BDQ et donner la valeur obtenue, arrondie au degré près.
d) Est-ce que la mesure de l’angle BDQ est égale au quart de la mesure de l’angle BDH ?
5) a) Placer sur la figure le point M sur la corde tel que BDM = MDH.
b) Mesurer sur la figure à quelle hauteur se trouvait Charles Poujade quand il était au point M (arrondir au mètre près).
Problème Niveau 3ème
Dans l’ensemble du problème, on arrondira les résultats obtenus au centième près.
Après 9 saisons, le record de vitesse pour la grimpée de la corde de 23 mètres a été établi en juillet 2024 par Charles Poujade en 22,70 secondes.
1) Quelle a été, en m/s, la vitesse moyenne de la grimpée de Charles Poujade ?
2) En admettant que la montée de Charles Poujade a été régulière, à quelle hauteur se trouvait-il au bout de 5 secondes ?
Dans les questions suivantes, aucune mesure sur la figure ne pourra servir de justification.
3) On a représenté, en Annexe, la corde de la Tour des héros par un segment vertical [BH] de longueur 23 m, B étant le point au sol et H le sommet. A 5 mètres du bas la corde, au sol, Denis Brogniart, le fameux présentateur de l’émission, regardait Charles grimper entre le point B et le point H. Denis se trouvait au point D.
Calculer la distance entre le lieu où se trouvait Denis Brogniart et le haut de la corde.
4) Calculer la mesure de l’angle BDH.
5) On appelle T le lieu où était Charles Poujade après avoir grimpé trois-quarts de la corde.
Calculer la mesure de l’angle DTH.
Annexe