Niveaux : 2 versions : Troisième et Terminale (Spécialité Maths)
Chapitres : Troisième : Trigonométrie, Théorème de Pythagore, Proportionnalité
Terminale : Géométrie dans l’espace
Inédit, publié le 19/03/2024

Note: sur la version en ligne du problème, les vecteurs sont écrits en gras italique.
Les spécialistes du handball parleront de ce tir encore pendant des décennies. Le 27 Janvier 2024, il ne restait au chronomètre qu’une seule seconde dans le temps règlementaire du match de la demi-finale des Championnats d’Europe de handball entre la France et la Suède. La Suède menait alors d’un but, quand la France obtint un coup franc. A plus de dix mètres du but, et malgré l’énorme mur et le brillant gardien suédois, Elohim Prandi pencha son corps et réussit l’exploit de marquer pour égaliser. La France finirait par remporter la victoire en prolongations, puis le trophée quelques jours plus tard. Légendaire !
Pour comprendre le problème, il est conseillé de regarder la vidéo du tir, disponible sur ce lien : https://ladigitale.dev/digiview/#/v/65f4b54fe40a5. On étudie dans ce problème la trajectoire du ballon égalisateur à partir du moment où il est lancé par Elohim Prandi(1).
Les deux problèmes proposés sont totalement indépendants (sauf l’utilisation de l’Annexe 1).
Niveau Troisième
Dans tout le problème, on arrondira les résultats obtenus au centième près.
Elohim Prandi, dans son lancer, se penche dans un plan incliné vers l’avant, étend son bras ce qui lui permet de contourner le mur de joueurs suédois face à lui. Au moment où le ballon quitte sa main, on estime que Elohim Prandi est penché de β = 35° par rapport au sol. La manière dont il est penché est visible en Annexe 1, dans le zoom visible en haut en droite.
1) Calculer, à partir de l’image de l’Annexe 1, la hauteur BH à laquelle le ballon se trouve quand il quitte la main de Elohim Prandi.
2) Calculer l’extension horizontale maximale du joueur donnée par la longueur AH.
3) On regarde maintenant la trajectoire du ballon, du point B au point C, lieu où le ballon touche la barre transversale, à 2 mètres de hauteur. On suppose que cette trajectoire est rectiligne. Au moment du lancer, le ballon se trouve à 9,60 mètres (à l’horizontale) de la cage adverse. La situation est représentée en Annexe 2.
Calculer la distance BC parcourue par le ballon.
4) Montrer que la mesure de l’angle γ que la trajectoire fait avec l’horizontale est d’environ 6°.
5) On a « flashé » le ballon de la trajectoire à une moyenne de 108 km/h. Combien de temps, en secondes, a-t-il mis pour parcourir la distance BC ?
Niveau Terminale
Dans tout le problème, on arrondira les résultats obtenus au centième près.
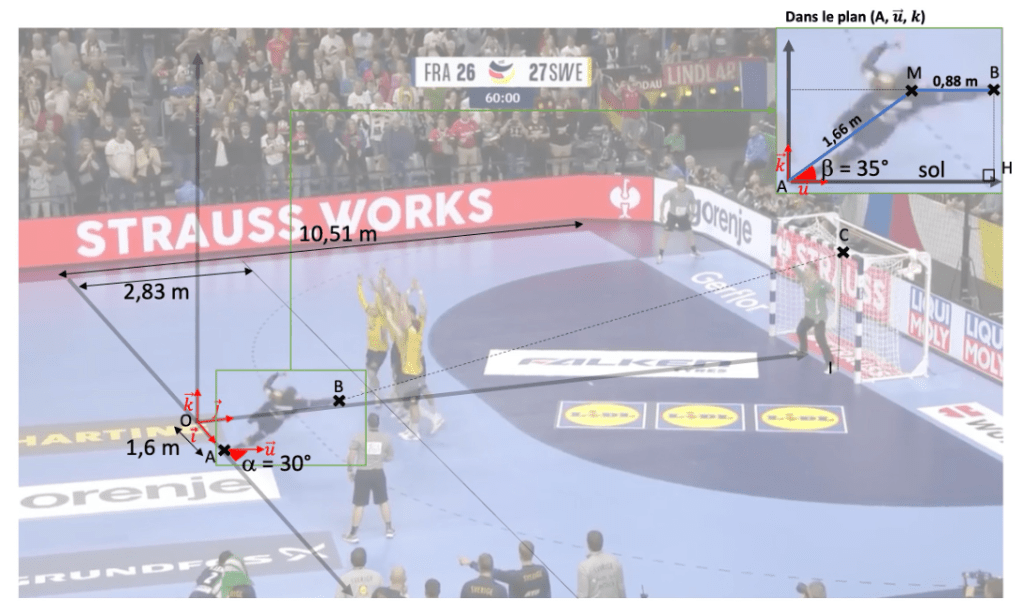
On définit un repère orthonormé (O, i, j, k), où O est un point situé sur la ligne qui coupe le terrain en deux en suivant la longueur du terrain, à exactement 10,51 m du but adverse. i et j sont respectivement dans la direction transverse et dans la longueur du terrain (O, i, j désignant donc le plan du terrain) et k est orienté à la verticale (voir Annexe 1). L’unité du repère est en mètres.
Elohim Prandi se trouve au point de départ dans le plan (O, i, k), peu importe où. Pour simplifier, on suppose que le joueur décale alors son pied droit en restant dans ce plan, prend appui sur ce pied au point A d’abscisse 1,6 sur l’axe des abscisses, puis se projette vers l’avant selon un plan (A, u, k), où u est un vecteur unitaire dans le plan du terrain avec α = (i, u) = 30°. Le corps du joueur fait alors un angle β = 35° avec le sol; son bras est étendu au maximum horizontalement pour faire partir le ballon d’un point B (voir l’image zoomée de l’Annexe 1, en haut à droite).
1) Donner, en fonction de l’angle α, les coordonnées du vecteur u dans le repère (O, i, j, k).
2) a) Déterminer les coordonnées du point B dans le plan (A, u, k).
b) En déduire les coordonnées de B dans le repère (O, i, j, k).
3) On admet que la trajectoire du ballon jusqu’à son entrée dans le but adverse est rectiligne. Très précisément, le ballon entre au point C – situé sur le dessous de la barre transversale – de coordonnées (1 ; 10,51 ; 2).
Donner dans le repère (O, i, j, k) une représentation paramétrique de la droite (BC).
4) a) Donner sans justifier les coordonnées respectives des projetés H et I des points B et C au sol, puis les coordonnées du vecteur HI.
b) Calculer le produit scalaire BC.HI.
c) En déduire que la mesure de l’angle γ que fait la trajectoire du ballon par rapport à l’horizontale est d’environ 6°.
5) a) On sait que le mur de joueurs suédois se situe exactement à 2,83 m devant Elohim Prandi. On suppose qu’il reste parallèle au plan (O, i, k), et qu’il peut être modélisé par un rectangle large de 3,42 m et haut de 2,88 m, en étant centré sur la ligne d’abscisse x = 0,7.
a) Quelles sont, dans le repère orthonormé (O, i, j, k), les conditions que respectent les coordonnées des points appartenant à ce mur ?
b) Déterminer à quelle distance à la droite du mur des joueurs suédois, puis à quelle hauteur, le ballon passe quand il traverse le plan de ce mur.
Annexe 1
Annexe 2 (uniquement pour le niveau 3ème)
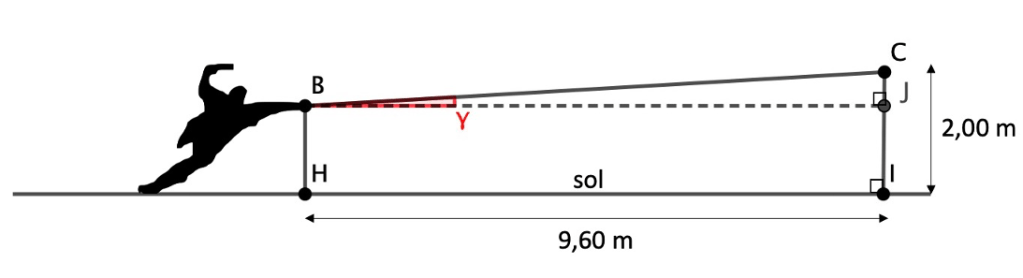
Remarque : Cette représentation est purement schématique. Elle n’est pas à l’échelle, et en réalité le corps de Elohim Prandi n’est certainement pas dans le plan où se trouvent les différents points du schéma.
(1) Source : https://www.france.tv/france-3/stade-2/5793579-elohim-prandi-description-d-un-geste-historique.html
Certaines données du problème sont issues de cette vidéo mais d’autres ont dû être estimées.