Niveaux : Troisième/Seconde
Chapitres : Pourcentages, Coefficient multiplicateur, Tableur, Algorithmique
Inédit, publié le 31/01/2023
Utilisable dans le cadre du passeport EDUCFI

Le sens de l’épargne se crée dès l’âge de 12 ans : c’est le but de l’existence du « Livret jeune ». Créé en 1996, il est disponible dans à peu près toutes les banques, et commence à rapporter de l’argent dès qu’un euro y est placé. Quel est l’intérêt réel de l’utiliser au lieu de laisser l’argent dans sa tirelire ? C’est ce que nous allons essayer de saisir dans ce problème.
Mettre de l’argent dans le livret jeunes est un placement, qui rapporte des intérêts, c’est-à-dire de l’argent supplémentaire. Le taux d’intérêt annuel du livret jeunes valait, début 2024, au minimum 3% : cela signifie que chaque euro présent dans le livret rapporte au minimum au bout d’un an, 3% de 1€, soit 3 centimes : on a alors 1,03 €. Les intérêts se cumulent : dans une deuxième année, le livret jeunes rapporterait, au minimum, sur ce même euro placé initialement : 1,03 € x 3% = 3,09 centimes supplémentaires etc…
Malone, un collégien, a placé 150 euros à l’ouverture d’un livret jeunes au tout début du mois de janvier 2024, au taux annuel de 3%. On suppose dans un premier temps que Malone n’ajoute pas d’argent dans son livret. On suppose de plus, même si ce n’est pas vrai dans la réalité, que le taux reste constant.
1) a) Par quel coefficient Malone devrait-il multiplier le montant placé initialement pour savoir ce qu’il contient au bout d’un an ?
b) En déduire le montant qui serait alors présent dans le compte de Malone au bout de 1 an, de 2 ans puis de 3 ans.
2) Dans le livret jeunes, les intérêts sont calculés par quinzaine: un euro commence à rapporter de l’argent à chaque moitié de mois, soit 24 fois par an. Pour la suite du problème, on supposera que le solde varie effectivement toutes les quinzaines, même si en réalité les intérêts ne sont crédités (c’est-à-dire visibles sur le compte) qu’en début de chaque année.
Malone pense que le taux d’intérêt appliqué à chaque quinzaine est égal à 3% ÷ 24, soit 0,125%.
a) Calculer ce que contiendrait le livret de Malone en appliquant ce taux d’intérêt sur 24 quinzaines.
b) En déduire que le raisonnement de Malone est erroné.
3) Pour trouver le taux correct en % à appliquer à chaque quinzaine, Malone utilise un tableur pour construire le tableau visible en Annexe 1. Il teste, dans la ligne 1 du tableau, différents taux d’intérêt par quinzaine et en déduit des taux annuels correspondant.
a) Quelles formules Malone a-t-il appliquées successivement dans les cellules B2, B3 et B4, avant de les étirer vers la droite ?
b) Lire dans le tableau de Malone le taux d’intérêt en % par quinzaine qui se rapproche le plus d’un taux correspondant au taux annuel de 3%, sans le dépasser.
4) Avec un sens de l’épargne, Malone commence à déposer, dès le début du mois de février 2024, 10 euros à chaque début de mois. Rappelons que cet argent déposé ne commence à produire des intérêts que dans la quinzaine qui suit.
a) A l’aide du taux trouvé dans la question 3.b), compléter et exécuter les programmes (Scratch ou Python) dans les fichiers associés au problème (429 – Programme.sb3 et 429 – Programme.py) ou en Annexe 2, pour déterminer en quel mois et en quelle année Malone aura dépassé le plafond du livret, c’est-à-dire 1 600 euros.
b) Comparer le temps qu’il aura gagné pour atteindre ce montant de 1 600 euros par rapport à construire une épargne similaire (150 euros initialement, puis 10 euros tous les mois) dans sa tirelire.
c) Conclure sur l’intérêt d’épargner avec ce livret.
Annexe 1

Annexe 2
Programme Scratch à compléter (pour les collégiens)
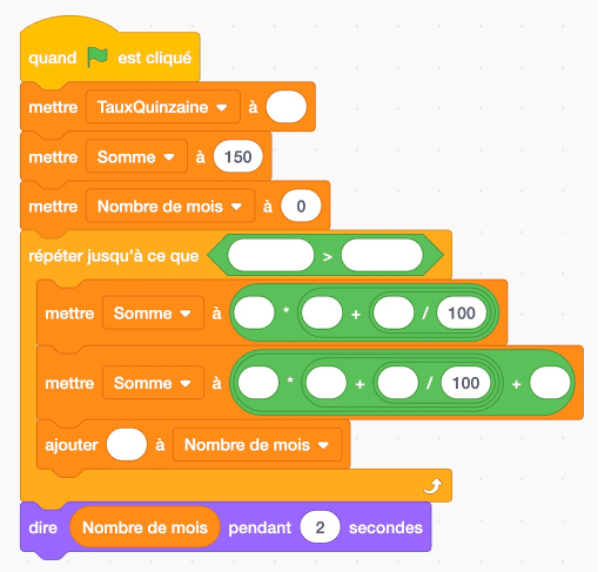
Programme Python à compléter (pour les lycéens)

Remarque aux enseignants : il existe bien sûr des formules exactes pour calculer le taux d’intérêt par quinzaine à partir du taux annuel, mais pas aux niveaux visés. L’objectif n’est pas ici d’utiliser les puissances fractionnaires ou les racines n-ièmes. Cependant, les enseignants qui le souhaiteront pourront certainement introduire ces notions pour les élèves les plus avancés ou motivés…