Problème 420 – La décoration parfaite du sapin de Noël

Niveaux : Quatrième
Chapitres : Proportionnalité, Calcul littéral, Tableur, Ratios
Inédit, publié le 25/12/2023

            La décoration parfaite du sapin de Noël existe-t-elle ? C’est en tout cas l’avis de membres de la Société de Mathématiques de l’Université de Sheffield, au Royaume-Uni⁽¹⁾. En 2012, cette société a publié des formules mathématiques permettant de calculer les valeurs idéales, en fonction de la taille du sapin, du nombre de boules, de la longueur des guirlandes, de la longueur des guirlandes lumineuses et même de la taille de l’étoile. Et c’est très sérieux puisque ces formules sont aujourd’hui utilisées dans des grands magasins pour leurs propres décorations de sapins. On se propose donc, dans ce problème, de jeter un coup d’œil sur ces formules.

1) Pour obtenir le nombre idéal de boules sur un sapin, on doit multiplier la hauteur du sapin en cm par √17 puis diviser le résultat obtenu par 20. On arrondit le résultat obtenu à l’entier près. 

Calculer le nombre idéal de boules pour un sapin mesurant 1,50 m.

2) On appelle la hauteur d’un sapin (en cm). Pour obtenir la longueur idéale L des guirlandes (en cm), on applique la formule suivante :

L = (13/8)πt.

a) Calculer L pour t = 150 (arrondir au cm près).

b) Calculer ce que serait la hauteur du sapin (arrondie au cm près) si la longueur idéale des guirlandes était de 5 mètres.

3) a) Dans le Tableau 1 ci-dessous, issu d’un tableur, quelle formule a-t-on entrée en cellule B2 avant de l’étirer verticalement ? 
Remarque : dans un tableur, π s’écrit PI().

b) Selon ce tableau, on a L = 102,10 pour t = 20. Qu’en pensez-vous ?

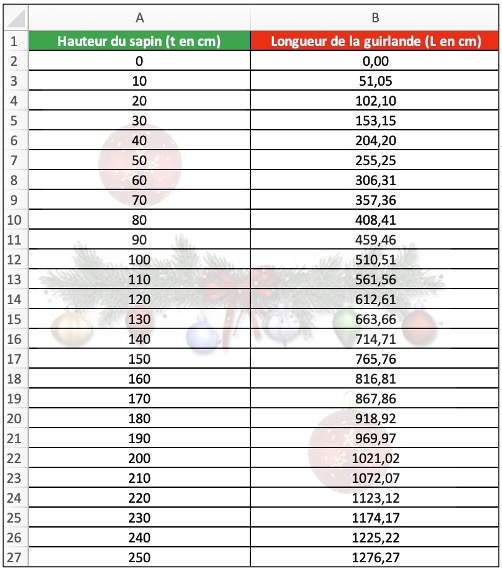
4) Si on devait tracer la représentation graphique de la longueur L des guirlandes en fonction de la hauteur du sapin t, quelle serait la forme de la courbe obtenue? Justifier la réponse. 

5) « La longueur idéale des guirlandes lumineuses est égale au périmètre d’un cercle dont le diamètre serait égal à la hauteur de l’arbre» (tout en cm). 

Déterminer le ratio entre la longueur idéale des guirlandes et celle des guirlandes lumineuses.

(1) Source : “Treegonometry creates perfect Christmas tree”, University of Sheffield, 28 Novembre 2012 (lien disparu, mais cité dans l’article suivant: https://newatlas.com/christmas-tree-decoration-mathematical-formula/25388/)