Problème 410 – Pandora n’est pas Gaïa

Niveau : Troisième
Chapitres : Volumes, Proportions, Grandeurs-quotient, Proportionnalité (Distance, Vitesse, Temps), Coefficient multiplicateur
Inédit, publié le 01/10/2023

            Dans l’univers des films Avatar du réalisateur James Cameron, Pandora est cette planète que les (méchants) humains veulent conquérir au détriment des (gentils) Navis (remarque : l’auteur du problème n’est pas spécialement fan de cette opposition plutôt binaire contenue dans les films…). Pandora n’est pas exactement une planète : elle est en réalité le satellite d’une planète, nommée Polyphemus, ce qui ne l’empêche pas d’être similaire à la Terre. Ou pas exactement, comme nous allons le voir dans ce problème.

            Pour simplifier notre comparaison, nous assimilons ici la Terre et Pandora à des globes. La Terre a un rayon de 6 371 km et on sait que Pandora a un rayon 10,17% inférieur⁽²⁾.

1) Rappeler par quel coefficient multiplicateur on obtient le rayon de Pandora à partir de celui de la Terre, puis calculer le rayon de Pandora en km.

2) Dans cette question on exprimera les résultats en km³, avec une notation scientifique.
a) Calculer le volume de la Terre.
b) Déterminer, de deux manières différentes, le volume de Pandora.

3) On rappelle que la masse volumique M d’un objet est donnée par la formule :

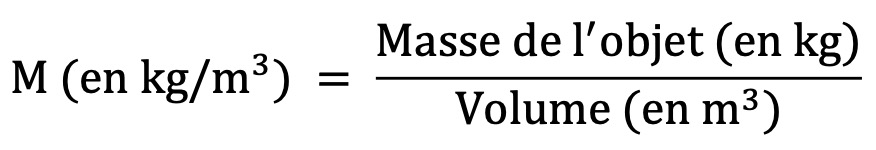
La Terre et Pandora ont respectivement des masses égales à 5,97 x 10²⁴ kg et 4,65 x 10²⁴ kg⁽²⁾.

Qui, de la Terre ou Pandora, a la masse volumique la plus grande ?

4) On donne, dans le Tableau 1 ci-dessous, les aires des surfaces émergées et immergées (couvertes d’eau) de la Terre et de Pandora⁽²⁾.

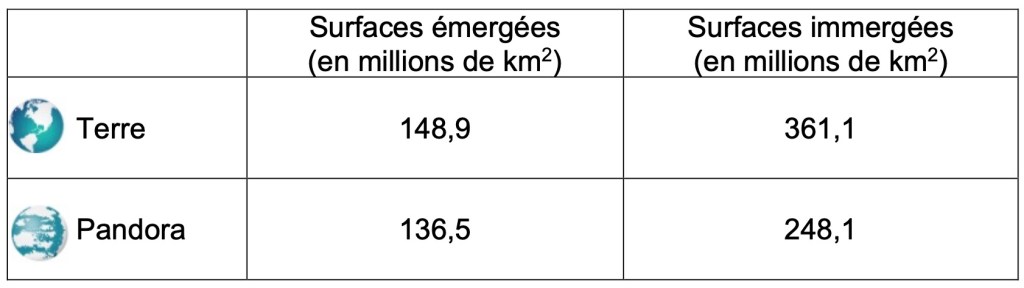
Qui, de la Terre ou Pandora, est celle qui, en proportion de sa surface totale, a la surface immergée la plus grande ? Justifier la réponse.

5) On suppose que la trajectoire de Pandora forme un cercle autour de Polyphemus. On sait que la vitesse de rotation de Pandora (son centre) autour de Polyphemus (son centre) est de 12,3 m/s⁽²⁾.

Montrer qu’il est impossible que Pandora fasse un tour de révolution autour de Polyphemus en 29,5 jours – comme la Lune le fait autour de la Terre.

Indication : on pourra faire un « raisonnement par l’absurde » : on suppose que cette possibilité est vraie, et on en déduit quelque chose d’impossible.

(1) Source : https://www.youtube.com/watch?app=desktop&v=REh_vObyh4g