Problème 389 – Touché, courbé!

Niveau : Première (Spécialité Maths)  
Chapitres : Polynômes du second degré, Nombre dérivé
Inédit, publié le 29/05/2023
Fait en collaboration avec Thomas Martin-Barbet , élève de 3^ème du collège Victor Duruy de Mont-de-Marsan

Remarque: ceux qui chercheront un problème très similaire pourront s’attaquer au problème 036 – Le menhir d’Obélix.

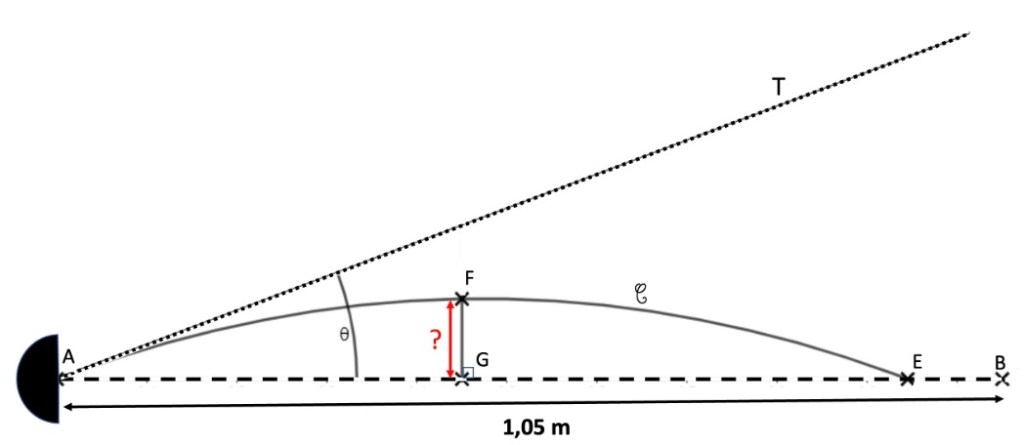
            En escrime, lorsque dans une distance courte, Lucille touche l’adversaire avec son épée, cette dernière peut se courber dans l’instant où la touche est effectuée. Cela ne dure qu’une fraction de seconde, mais cela est souvent suffisant pour que le point soit marqué. On se propose, dans ce problème, de modéliser la manière dont l’épée se courbe.

            Cette modélisation est visible sur le schéma en Annexe. On considère que la lame de l’épée de Lucille, longue de 1,05 m, indiquée en pointillés par le segment [AB], se courbe le long d’une portion de parabole Centre les points A et E : E est donc le point où la touche se produit. E est tel que E ∈ [AB] et tel que la longueur AE vaille 90% de la longueur de la lame. Quand cela se produit, on admet alors que la tangente à la parabole en A fait un angle θ égal à 44° par rapport à (AB)^(*). 

            On appelle F le sommet de la parabole C, et G la projection orthogonale de F sur (AB). L’objectif de ce problème est de déterminer de quelle hauteur [FG] l’épée se courbe lorsque Lucille touche son adversaire de cette manière.

Note : pour un élève de niveau avancé, l’énoncé est déjà suffisamment complet pour être résolu. 

Résolution avec des questions guidées

On suppose que l’origine de l’épée A se trouve à l’origine d’un repère orthogonal centré en A, où l’unité est le mètre et où l’axe des abscisses est représentée par l’axe (AB). On modélise la trajectoire de l’épée courbée C par une parabole d’équation f(x) = ax² + bx + c tracée entre les points A et E.

1) Déterminer les coordonnées de A, B et E dans le repère indiqué.

2) Justifier que G est le milieu de [AE].

3) Dans l’expression de f, déterminer la valeur de c.

4) a) Exprimer la valeur de f'(0) en fonction de b.

b) En déduire la valeur de b.

5) Calculer la valeur de a.

6) Conclure en calculant l’ordonnée du sommet de la parabole.

Annexe
Le schéma est indicatif et n’est pas à l’échelle

(*) Note : ceux qui ont un niveau (bien) plus avancé en mathématiques pourront vérifier que la longueur de la portion de courbe est bien proche de 1,05 m.